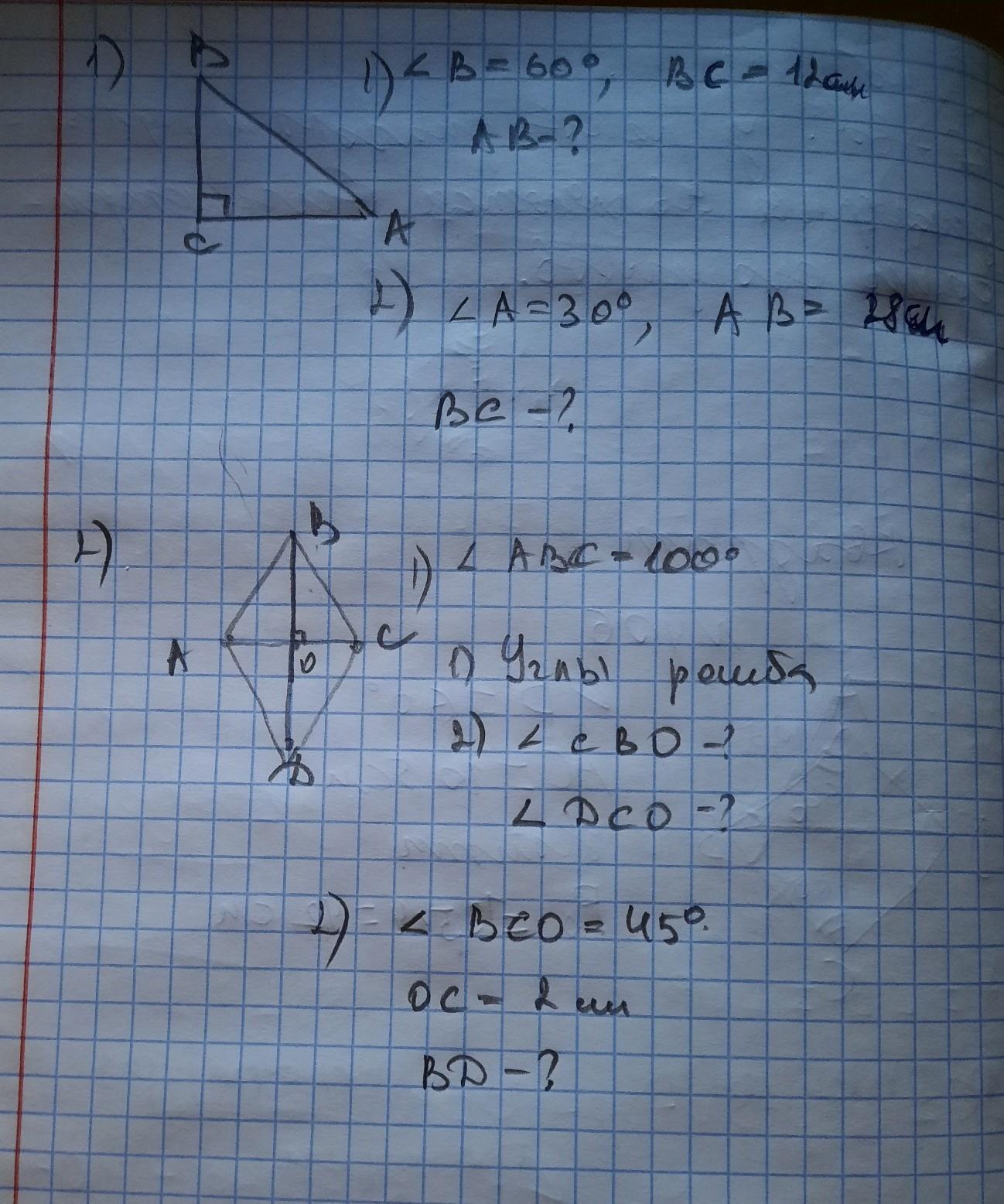Ответы
Ответ:
Объяснение:
В прямоугольном треугольнике против угла 30 градусов лежит катет равный половине гипотенузы. Эта теорема используется в первых двух заданиях.
1. Если угол В = 60, то по теореме о сумме острых углов прямоугольного треугольника равных 90 градусам, то угол А равен 30 градусам. Тогда АВ = 2ВС = 2*12 = 24.
1.2 Аналогично, ВС = АВ/2 = 28/2 = 14
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
2. Значит угол СВО = 100/2 = 50 градусам.
Так как противолежащие углв ромба равны, то и угол СДО = 50 градусам. Тогда в прямоугольном треугольнике ДОС угол ДСО = 90 - 50 = 40 градусам.
2.1 Угол ВСО = 45 градусам. Тогда углы всех треугольников, на которые разделили ромб его диагонали равны 45 градусам. Значит они равнобедренные и их катеты равны. Равны и острые углы получившихся треугольников.
угол СВО = углу ДСО = 45 градусам.
2.2 Ну, очевидно, так как у равнобедренного прямоугольного треугольника катеты равны, то ОС = ВД = 2
Ответ:
Объяснение:
1 . 1) ∠A = 90° - ∠B = 90° - 60° = 30° . ∠A = 30° , тому ВС = 1/2 АВ;
АВ = 2* ВС = 2 * 12 = 24 ( см ) ; АВ = 24 см .
2) АВ = 28 см ; ∠А = 30° , тому ВС = 1/2 АВ = 1/2 *28 = 14 ( см ) ;
ВС = 14 см .
2 . 1) У ромбі ABCD ∠ABC = 100° . ∠ABC = ∠ADC = 100° .
За властивістю паралелограма ∠АВС + ∠BCD = 180°;
∠BCD = ∠BAD = 180° - ∠ABC = 180° - 100° = 80°.
2) ∠CBO = 1/2 ∠ABC = 1/2 * 100° = 50° ; ∠DCO = 1/2 * 80 = 40° .
3 . У ромбі ABCD ∠BCO = 45° ; OC = 2 см . ΔВСО - прямокутний
рівнобедрений , тому ОС = ОВ = 2 см . BD = 2*OB = 2*2 = 4 ( см ) .