Ответы
Ответ дал:
0
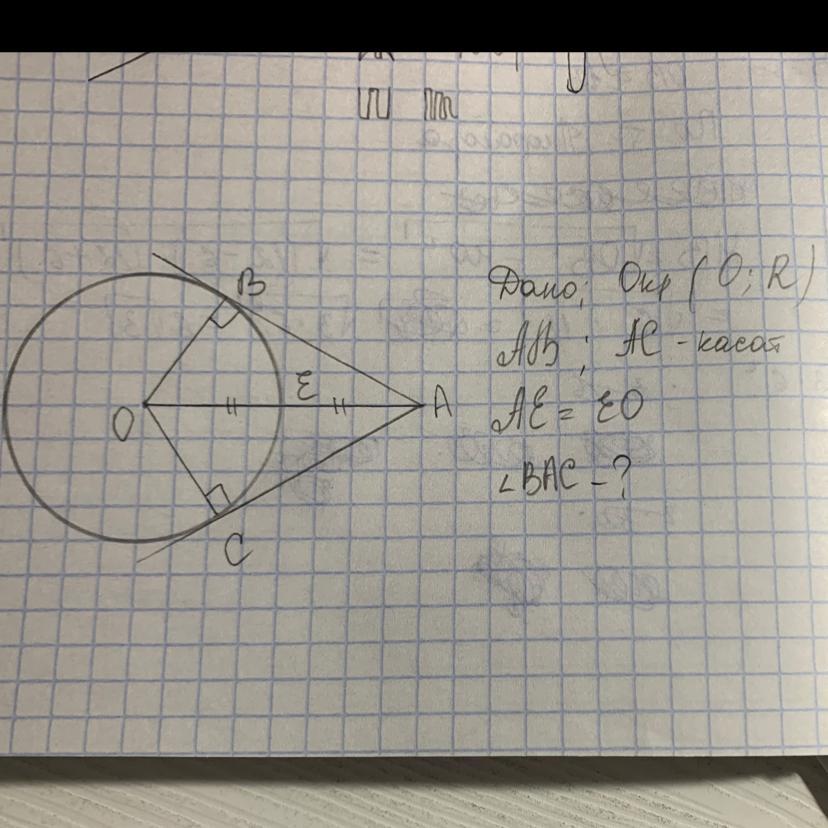
Т.к. АС и АВ - касательные, проведенные из одной точки, то ОВ⊥АВ, ОС⊥АС.
Т.к. ОЕ=ЕА=ОВ=R, то ОВ=0.5ОА⇒∠ВАО=30°, а т.к. АО - биссектриса угла ВАС, ( это следует из равенства треугольников, они равны по катету= радиусу и гипотенузе - отрезкам касательных, до точки касания), то ∠ВАС=2*30°=60°
Ответ 60°
Ответ дал:
0
Ответ:
ОА=ОЕ+АЕ или же как 2r
Углы ОСА=90°(по свойству касательных)
OC==1/2 AO=угол OAC=OBA=30°
Угол ОАС=углу OAB(по свойству отрезков касательных)
Из всего этого следует, что
Угол ВАС=2*угол ОАС=2*30=60°
Ответ :угол ОАС=60°
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад