Question

Помогите! Геометрия 7 класс (50 баллов)
Пожалуйста можно с подробным решением.

Answer 1

Ответ:

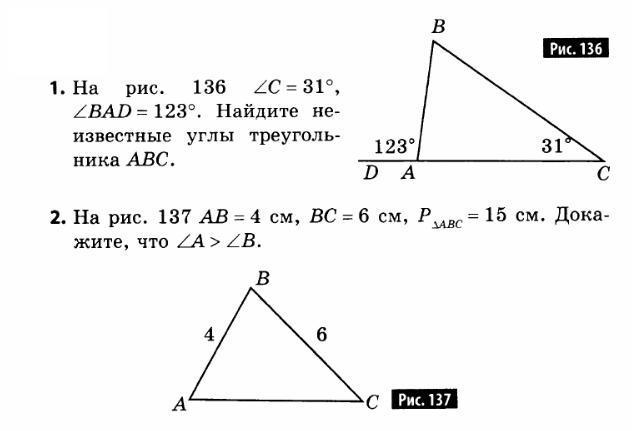
1. Неизвестные углы треугольника:

∠ВАС = 57°; ∠В = 92°.

2. Доказано, что ∠А > ∠B

3. Углы треугольника АВС равны 70°, 55°, 55°.

Объяснение:

1.

Дано: ΔАВС.

∠С = 31°; ∠BAD = 123°;

Найти: неизвестные углы треугольника:

∠ВАС; ∠В.

Решение:

• Сумма смежных углов равна 180°.

⇒ ∠ВАС = 180° - ∠DAB = 180° - 123° = 57° (смежные)

• Внешний угол треугольника равен сумме углов, не смежных с ним.

⇒ ∠В = ∠DAB - ∠С = 123° - 31° = 92°

Неизвестные углы треугольника:

∠ВАС = 57°; ∠В = 92°.

2.

Дано: ΔАВС;

АВ = 4 см; ВС = 6см;

Р (АВС) = 15 см.

Доказать, что ∠А > ∠B.

Доказательство:

• Периметр треугольника - сумма длин всех сторон.

Р(АВС) = АВ + ВС + АС

15 = 4 + 6 + АС

АС = 5 (см)

• В треугольнике против большей стороны лежит больший угол.

ВС > AC (6 см > 5 см)

⇒ ∠А > ∠B

Доказано, что ∠А > ∠B

3.

Дано: ΔАВС;

АВ = ВС;

∠DBC = 110°

Найти: углы треугольника АВС.

Решение:

Рассмотрим ΔАВС - равнобедренный.

∠АВС = 180° - ∠DBC = 180° - 110° = 70° (смежные)

• В равнобедренном треугольнике углы при основании равны.

⇒ ∠А = ∠С

• Сумма углов треугольника равна 180°.

⇒ ∠А = ∠С = (180° - ∠АВС) : 2 = (180° - 70) : 2 = 55°

Углы треугольника АВС равны 70°, 55°, 55°.