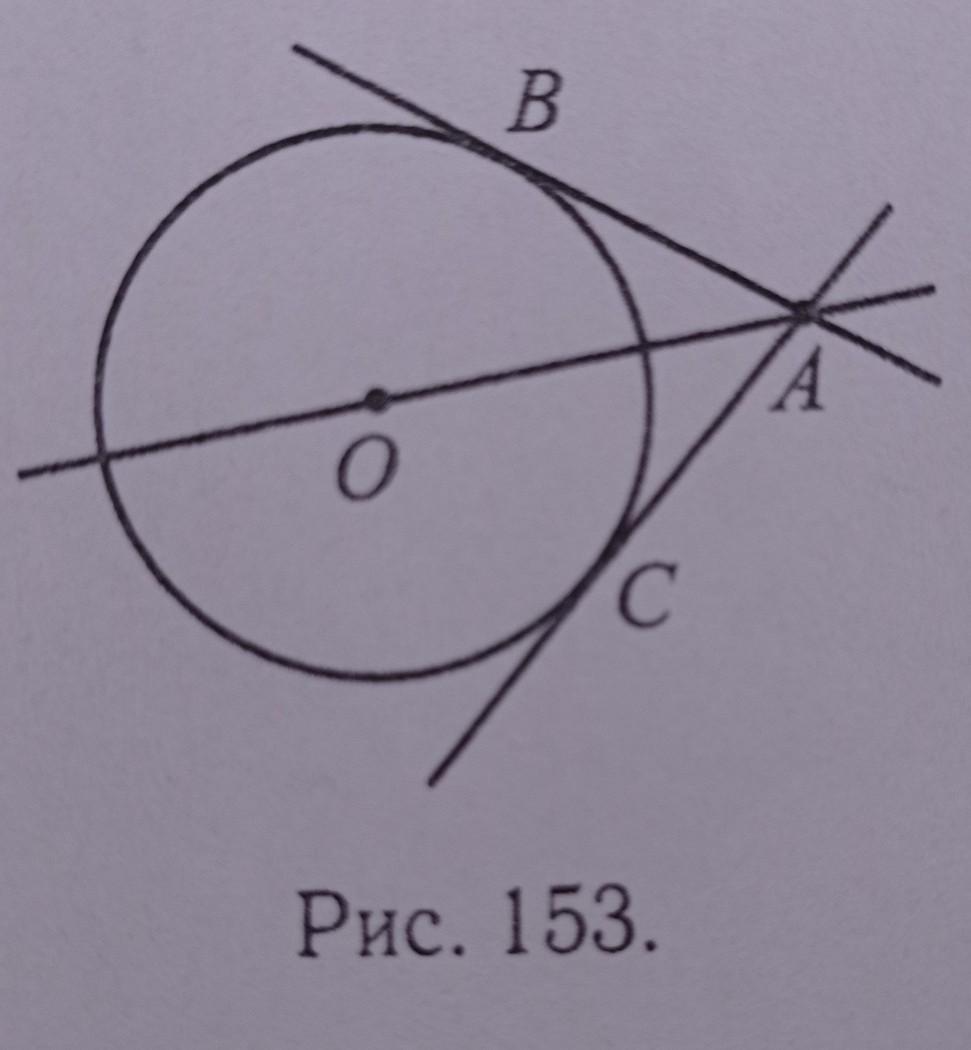
Дана окружность с центром О и радиусом 8 и точка А (см. рис. 153). Прямые AC и AB касаются окружности в точках С и В. Найдите OA, если угол ВАО = 45°.
Приложения:
zmeura1204:
8√2
Ответы
Ответ дал:
3
Ответ: 8√2
Объяснение:
радиус ОВ перпендикулярен АВ, т.к. он проведен в точку касания, если соединить токи О и ВЮ получим прямоугольный равнобедренный треугольник, т.к. дан по условию угол ВАО = 45°.Ю а угол АВО=90°, значит, и ∠ВОА=45°, т.к. сумма острых углов в прямоугольном треугольнике равна 90°, значит, гипотенуза ОА равна ОВ/sin∠ВАО=8/(sin45°)=8/(1/√2)=8√2
второй способ по теореме Пифагора √(8²+8²)=8√2
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад