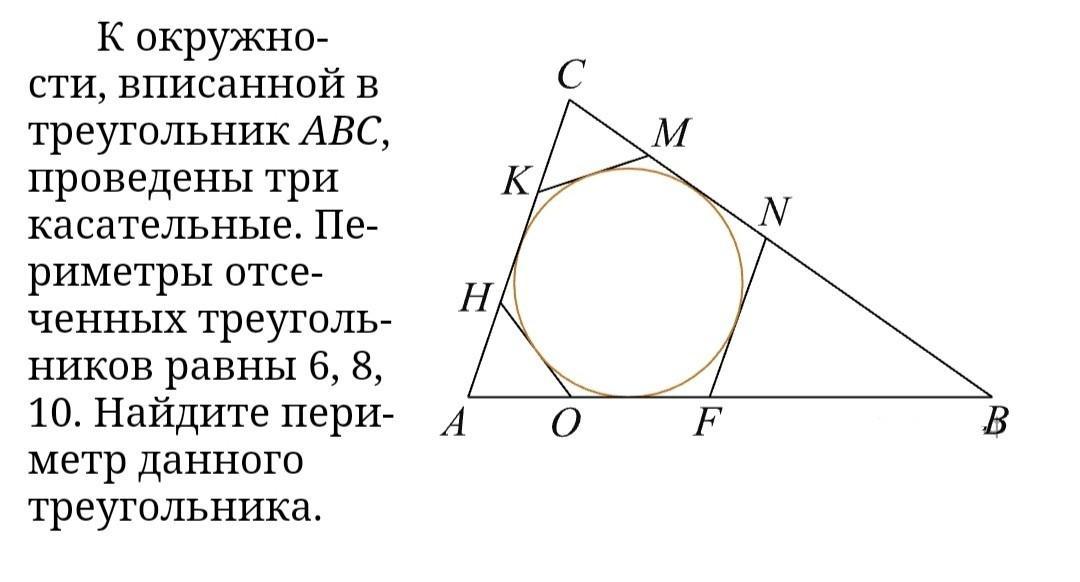
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
Приложения:
Ответы
Ответ дал:
0
Ответ:
Допустим см,
см,
см.
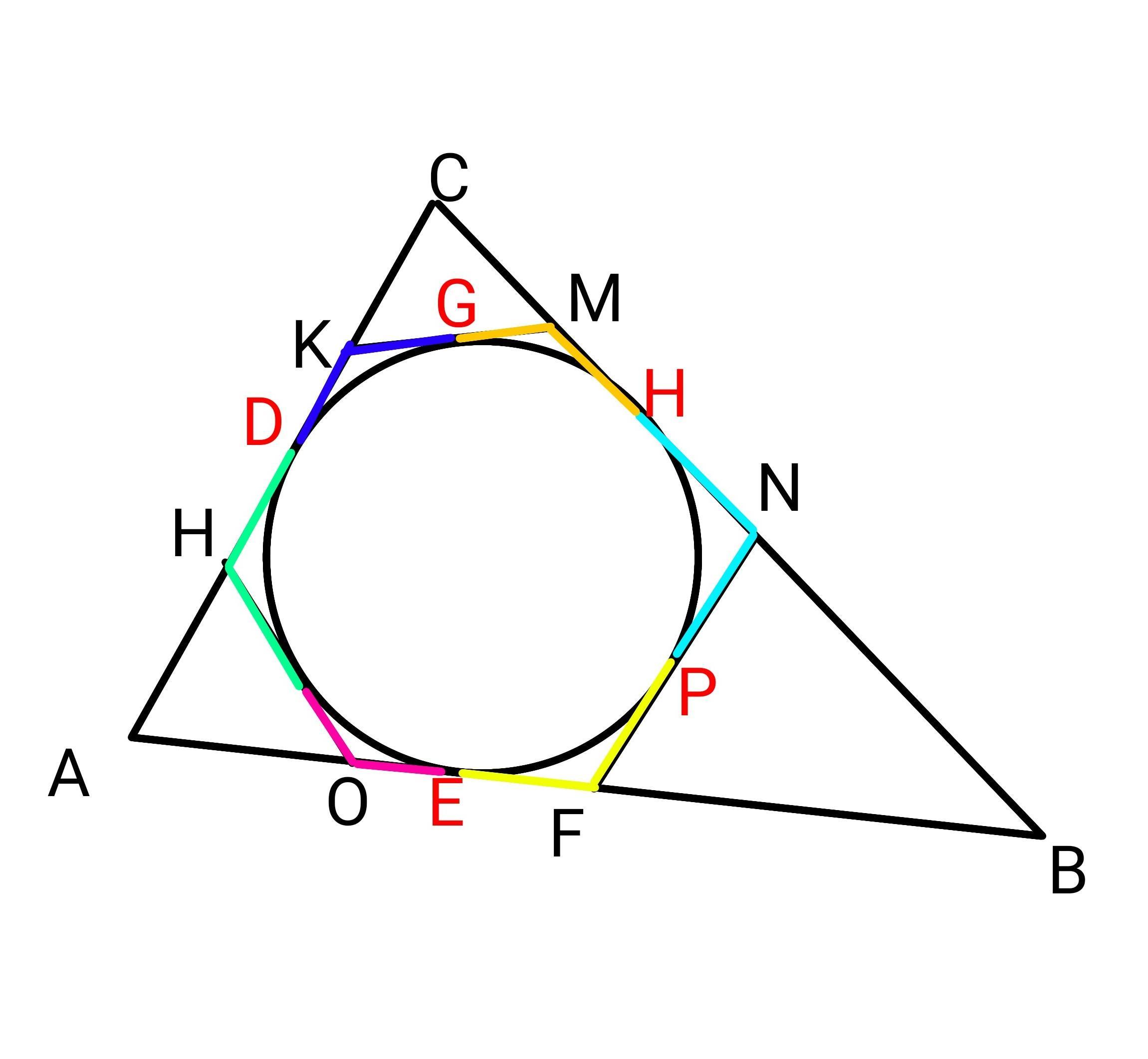
Касательные к окружности из одной точки равны. Обозначим точки касания окружности буквами D, G, H, P, E, F. (Извиняюсь, я забыл обозначить буквой между отрезком OH, обозначим его как F)
Все равные отрезки: HF=HD, KD=KG, MG=MH, NH=NP, FP=FE (я их отметил разными цветами).
Так как OH=HD+OE,
KM=KD+MH,
NF=NH+FE,
Поэтому периметр ΔABC равняется сумме периметров отсеченных треугольников.
см
Приложения:
bertramjeratire:
Блин, я сейчас заметил, что там буква H повторяется, но надеюсь понятно
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад