Ответы
Ответ дал:
0
Ответ:
ВС= 10 ед. - боковая сторона треугольника
Объяснение:
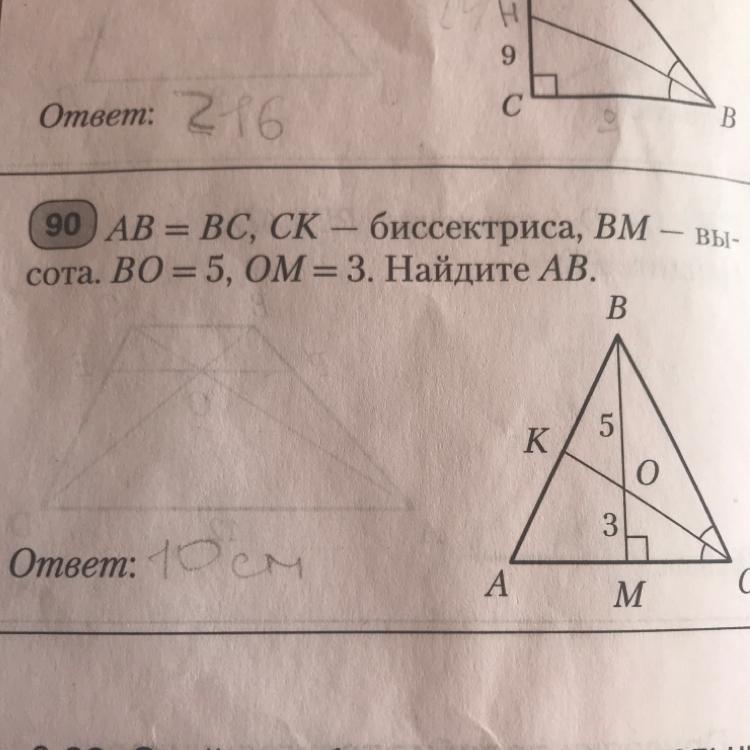
Дан Δ АВС -равнобедренный. В нем проведена биссекриса СК и высота ВМ. Они пересекаются в точке О, так что ВО=5, ОМ =3.
СО это будет биссектриса треугольника ΔСМВ.Воспользуемся свойством биссектрисы.
Биссектриса треугольника делит противолежащую сторону на отрезки пропорциональные сторонам.
Тогда
Пусть сторона ВС= 5х, МС= 3х. Тогда к Δ ВМС - прямоугольному применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Условию задачи удовлетворяет только положительное число х= 2.
Тогда .
Δ АВС -равнобедренный.
Значит, АВ= ВС= 10 ед.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад