Question

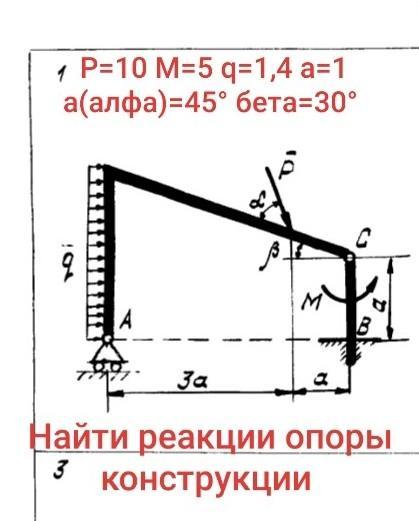
Помогите пожалуйста решить задачу еще раз zinovicgrigoij ​

Answer 1

Ответ:

Объяснение:

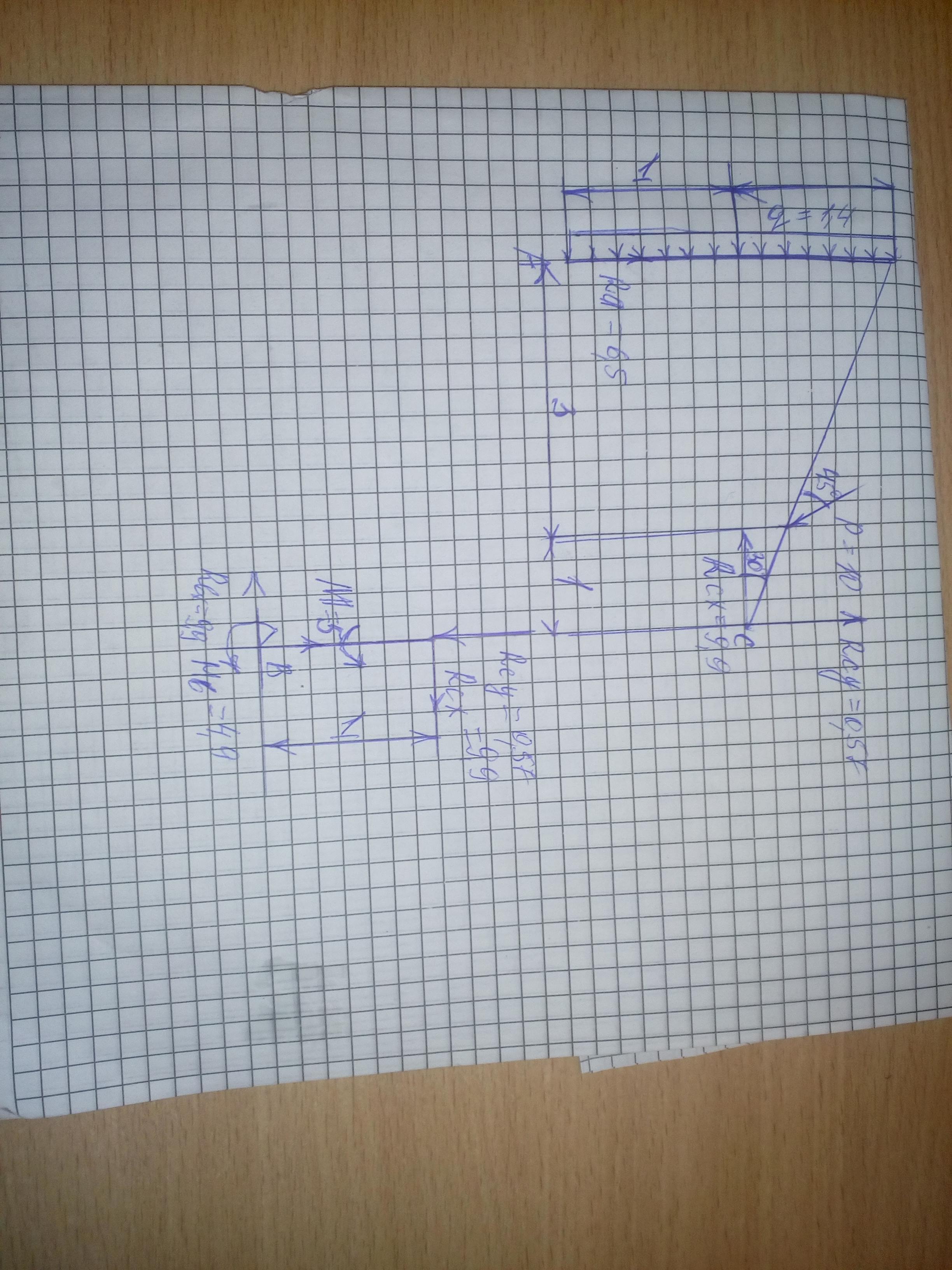
Находим длину вертикальной балки над опорой А

l=a+3a*tgβ=1+3*tg30°=2,7

Разделяем конструкцию на шарнире С и направляем реакции шарнира по по оси Х влево, по оси Y вверх.

Составим проекцию сил на ось Х и найдем реакцию Rcx

∑Fx=0; ql+Pcosα*cosβ-Rcx=0

Rcx=1,4*2,7+10*сos45*cos30=9,9

Составим уравнение моментов относительно опоры А и найдем реакцию шарнира Rcy

∑Ma=0; Rcy*4a+Rcx*a-Psinα*3a-ql*l/2=0

Rcy*4+9,9*1-10*sin45°-1,4*2,7*2,7/2=0

Rсy=0,57

Cоставим проекцию сил на ось Y и найдем реакцию опоры Ra, направим реакцию опоры вверх:

∑Fy=0; Ra-P*sinα+Rcy=0

Ra-10*sin45°+0,57=0

Ra=6,5

Проверка:

6,5-10*sin45°+0,57=0

0=0

Реакции найдены правильно.

Переходим ко второй части конструкции.

Реакции шарнира С будут направлены в противоположную сторону.

Составим уравнение сил относительно оси Х и найдем Rвх, направим Rвх влево:

∑Fx=0; -Rвx+Rcx=0

Rвх=Rcx=9,9

Составим уравнение сил относительно оси Y и найдем реакцию опоры Rвy, Rвy направим вверх:

∑Rвy=0; Rвy-Rcy=0

Rвy=Rcy=0,57

Составим уравнение моментов относительно опоры В и найдем удерживающий момент опоры В, момент направим против часовой стрелки:

∑Мв=0; М1+М-Rcx*a=0

M1=Rcx*a-M=9,9-5=4,9