8 класс. две окружности с радиусом 8 и 9 касаются внешним образом. Из центра меньшей окружности проведена касательная к большей а из полученной точки касания проведена вторая касательная к первой окружности. Найдите длину второй касательной. (Рисунка нет) даю 50 баллов (На русском языке) СРОЧНО!!!!
Ответы
Ответ дал:
3
Ответ:
Длина второй касательная равна 12 см.
Объяснение:
- Окружности касаются внешним образом, если они расположены вне друг друга.
Окружность с центром в точке А касается окружности с центром в точке В. К - точка касания.
Радиус первой окружности равен 8 ед, радиус второй - 9 ед.
Расстояние между центрами окружностей, касающихся внешним образом равно сумме их радиусов:
АВ=АК+КВ=8+9=17 ед.
АС - касательная, проведенная из центра меньшей окружности к большей. С - точка касания.
- Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания (свойство касательной).
Следовательно АС⟂ВС.
Рассмотрим прямоугольный треугольник АВС(∠С=90°).
По теореме Пифагора:
АС²=АВ²-ВС²=17²-9²=289-81=208.
Из точки С проведена вторая касательная к первой окружности. D - точка касания.
По свойству касательной: DC⟂AD.
Рассмотрим прямоугольный треугольник АДС(∠D=90°).
Катет DC найдём по теореме Пифагора:
DC²=AC²-AD²=208-8²=208-64=144
DC=12 ед.
Приложения:
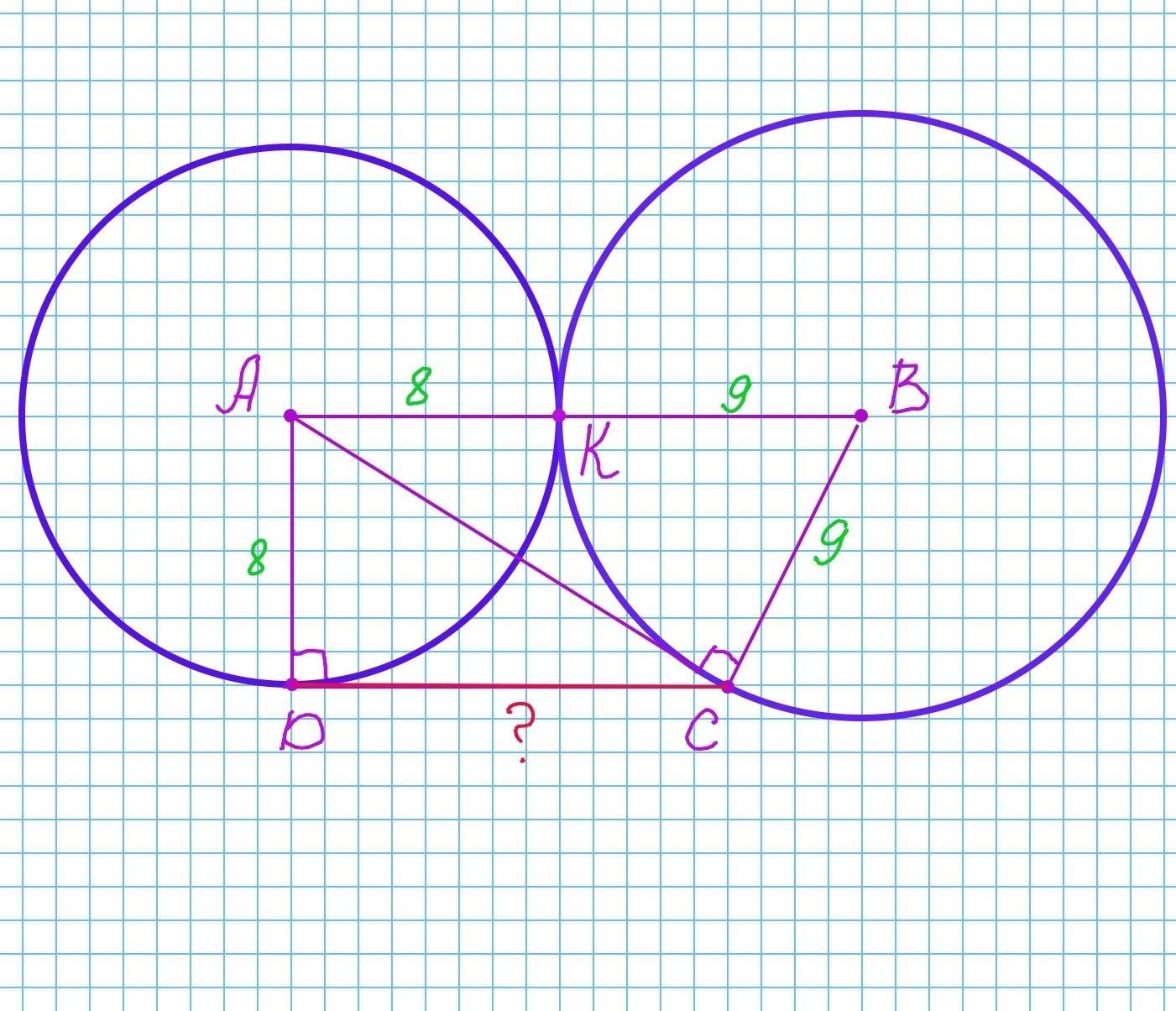
orjabinina:
Длина второй касательнОЙ
Автоисправление. Не увидела...
у меня тоже часто бывает.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад