катеты прямоугольного треугольника 6 и 8 дм а его гипотенуза 10 дм Найдите высоту проведенную из вершины прямого угла на гипотенузу
Ответы
Ответ дал:
1
Воспользуемся формулами площади и прямоугольного Δ
где S - площадь Δ; с - гипотенуза; h - высота; a и b - катеты, соответственно
Ответ. 4,8 дм.
Лучший ответ пж
Ответ дал:
1
Ответ:
h = 4,8 дм
Объяснение:
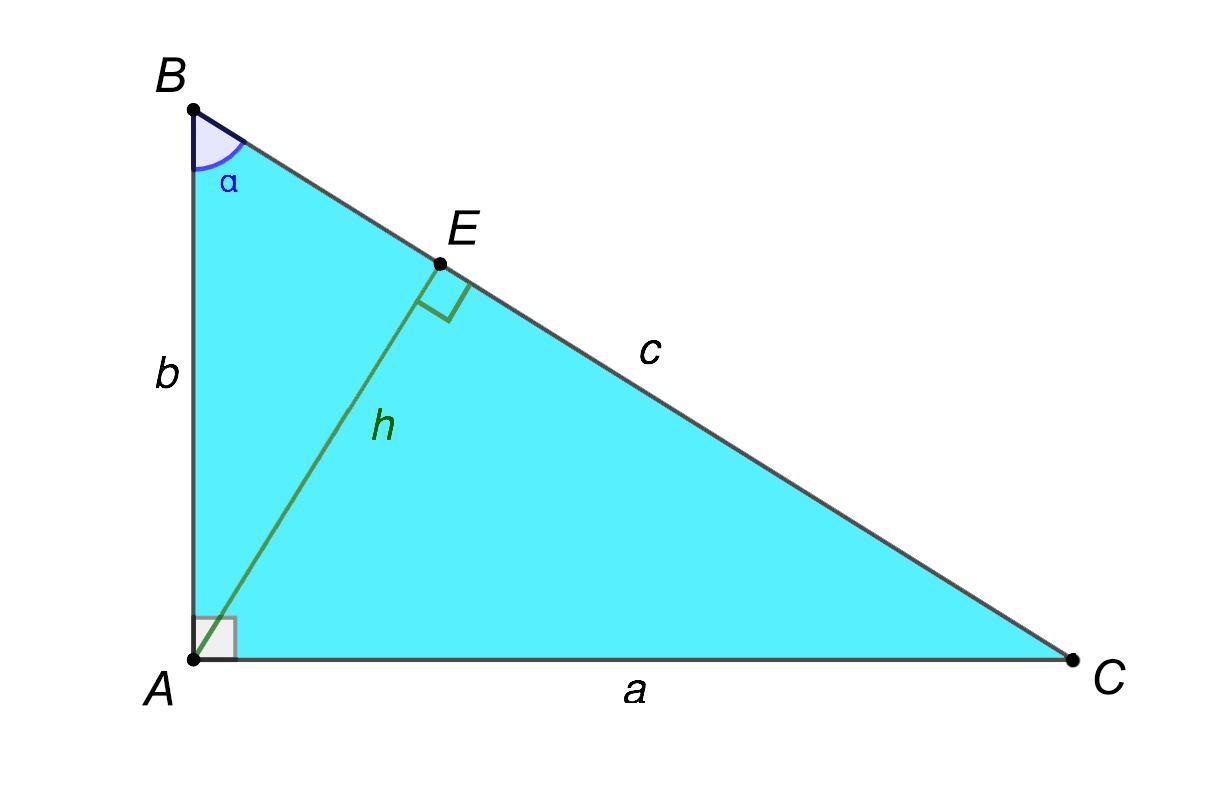
Рассмотрим ΔABC - Это прямоугольныйтреугольник.
У него:
Рассмотрим ΔABE - Это тоже прямоугольныйтреугольник.
У него:
Так как ∠α общий ⇒ sin(α) в обеих треугольниках торавны, ⇒
Найдём высоту h:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад