Question

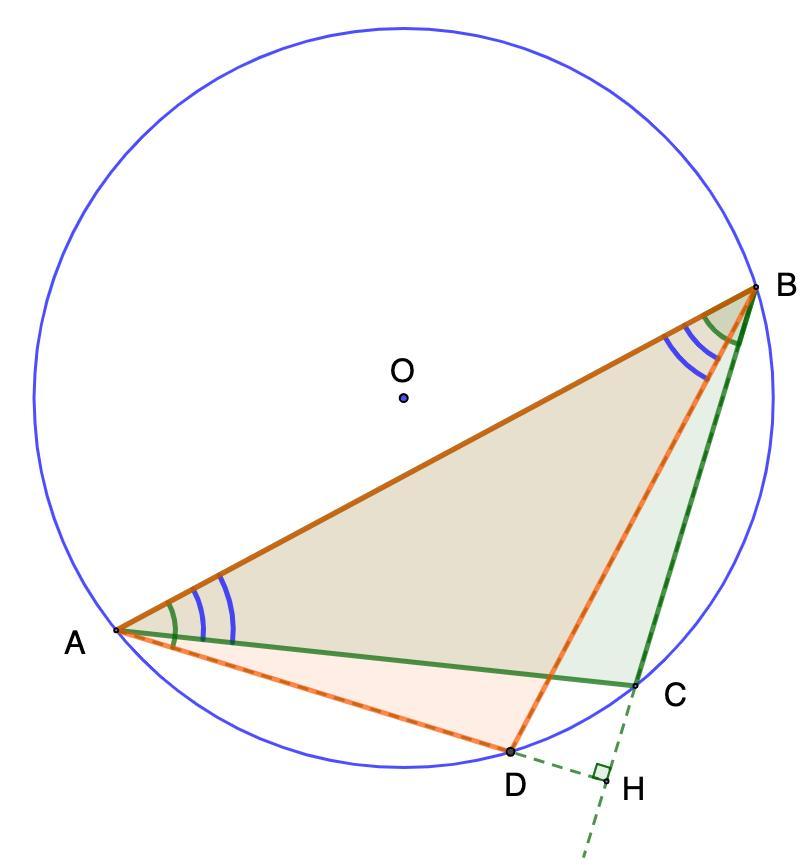
В треугольнике ABC угол C — тупой, угол B равен 45° и AH — высота. Прямая AH пересекает описанную около треугольника ABC окружность в точке D.

а) Докажите, что дуги BC и DA равны.

б) Найдите BC, если AC = 8 и площадь треугольника BDH равна 9.

Answer 1

Ответ:

а) Доказано, что дуги BC и DA равны.

б) ВС равно 2√7 ед.

Объяснение:

Требуется доказать, что дуги BC и DA равны.

Найти BC, если AC = 8 и площадь треугольника BDH равна 9.

Дано: ΔАВС - тупоугольный, ∠С - тупой.

∠В = 45°, АН - высота.

АН ∩ Окр.О = D;

AC = 8; S(BDH) = 9

Доказать: ◡BC = ◡DA;

Найти: ВС.

Доказательство:

1. Рассмотрим ΔАВН - прямоугольный (АН - высота).

∠В = 45°.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠А = 90° - 45° = 45°

• Если в треугольнике два угла равны, то он равнобедренный.

⇒ ΔАВН - равнобедренный.

2. Рассмотрим ΔADB и ΔACB.

АВ - общая;

∠А = ∠В = 45°

• Вписанные углы, опирающиеся на одну дугу, равны.

⇒ ∠DAC = ∠DBC (вписанные, опираются на ◡DC).

∠САВ = ∠А - ∠DAC

∠DBA = ∠B - ∠DBC

• Если правые части равенства равны, то равны и левые.

⇒ ∠САВ = ∠DBA

ΔADB = ΔACB (по стороне и двум прилежащим к ней углам, 2 признак)

⇒ AD = CB (как соответственные элементы)

• Равные хорды стягивают равные дуги.

⇒ ◡AD = ◡CB

Решение:

1. Рассмотрим ΔАСН и ΔDBH - прямоугольные.

АН = НВ (ΔАВН - равнобедренный)

∠DAC = ∠DBC (вписанные, опираются на ◡DC).

ΔАСН = ΔDBH (по катету и острому углу)              

⇒ DH = HC; HB = AH; DB = AC (как соответственные элементы)

Пусть меньшие катеты ΔАСН и ΔDBH равны:

DH = HC = x

Большие катеты равны:

АН = НВ = y

Гипотенузы:

AC = DB = 8

S(DBH) = S(АСН) = 9

2. Рассмотрим ΔDBH - прямоугольный.

• Площадь прямоугольного треугольника равна половине произведения катетов.

$\displaystyle S(DBH) = \frac{1}{2}\cdot{xy} \\\\9=\frac{1}{2}xy\\ \\\boxed {xy=18}$

По теореме Пифагора:

DH² + HB² =  DB²

$\displaystyle \boxed {x^2+y^2=64}$

Решим систему уравнений:

$\displaystyle \left \{ {{xy=18} \atop {x^2+y^2=64}} \right.$

Умножим первое уравнение на 2 и сложим уравнения:

$\displaystyle + \left \{ {{xy=18\;\;\;|\cdot2} \atop {x^2+y^2=64}} \right.\\\\x^2+2xy+y^2=100\\\\(x+y)^2 = 100\\\\x+y = 10\\\\x=10-y$

Отрицательные значения не берем, так не подходят по условию.

Стороны - величины положительные.

Подставим значение х в первое уравнение:

$\displaystyle (10-y)\cdot{y}=18\\\\10y-y^2-18=0\\\\y^2-10y+18 = 0\\\\D=100-4\cdot18 = 28\\\\\sqrt{D}=2\sqrt{7}\\ \\ y_1=\frac{10+2\sqrt{7} }{2}=5+\sqrt{7}\\ \\ y_2=\frac{10-2\sqrt{7} }{2}=5-\sqrt{7}$

Найдем x:

x₁ = 10 - 5 - √7 = 5 - √7

x₂ = 10 - 5 + √7 = 5 + √7

Так меньший катет DH, то возьмем пару:

DH = НС = x = 5 - √7

НВ = у = 5 + √7

ВС = НВ - НС =  5 + √7 -  5 + √7 = 2√7

ВС равно 2√7 ед.