Question

Натуральное число при делении на 5 даёт в остатке 4. Докажите, что сумма куба этого числа и его квадрата делится на 5.

Answer 1

Ответ:

Пошаговое объяснение:

смотри

Answer 2

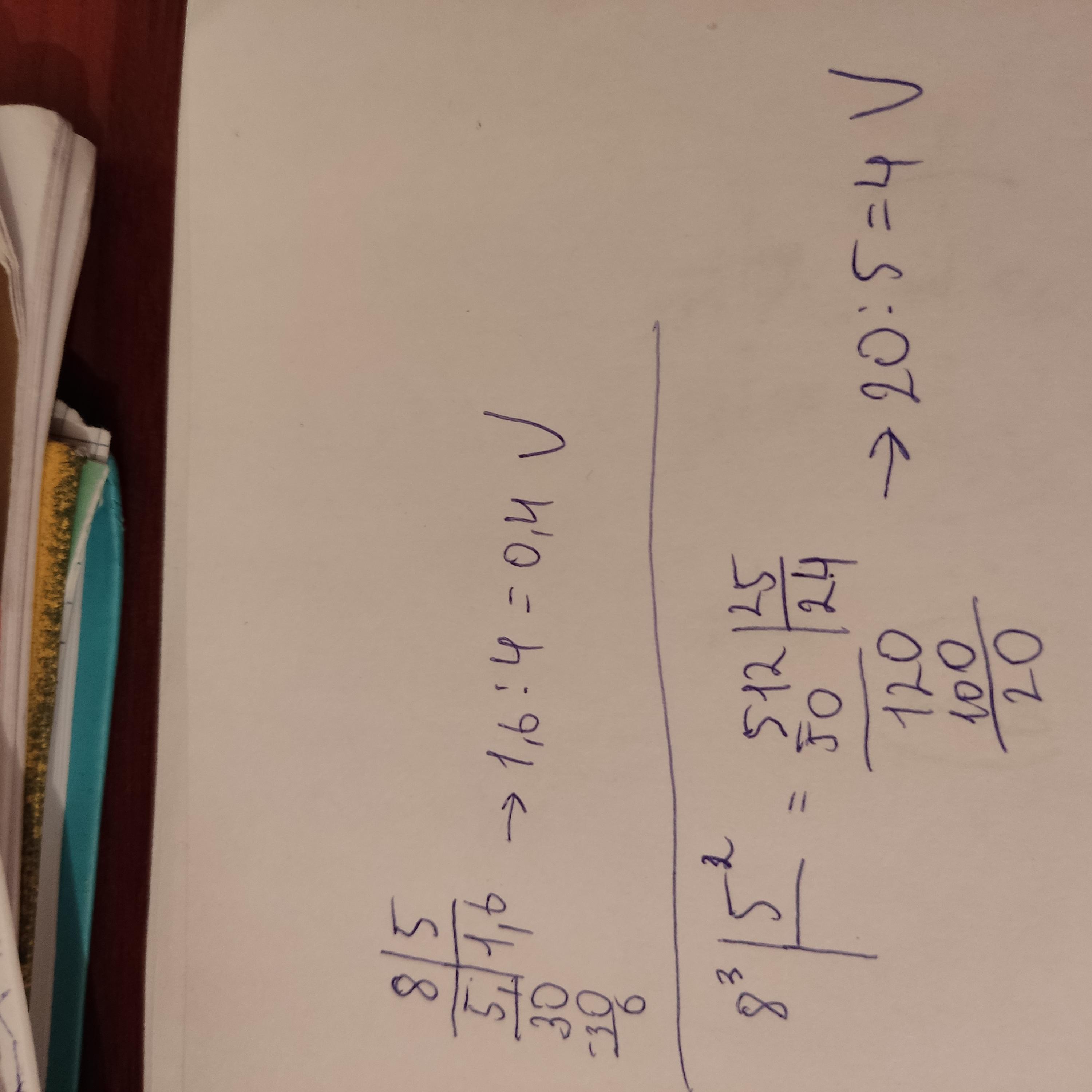
Пусть перед нами натруальное число n. По условию при делении n на 5 имеем остаток 4, то есть n сравнимо с 4 по модулю 5 ($n \equiv 4$ $mod$ $5$). Тогда $n^2 \equiv 4^2$ $mod$ $5$, то есть $n^2 \equiv 16$ $mod$ $5$, и $n^3 \equiv 4^3$ $mod$ $5$, то есть $n^3 \equiv 64$ $mod$ $5$. Тогда $(n^3+n^2) \equiv (64+16)$ $mod$ $5$, то есть $(n^3+n^2) \equiv 80$ $mod$ $5$. Но $80 \equiv 0$ $mod$ $5$. Тогда $(n^3+n^2) \equiv 0$ $mod$ $5$, что равносильно тому, что $(n^3+n^2)$ дает остаток 0 при делении на 5, то есть $(n^3+n^2)$ делится на 5. Что и требовалось доказать.

Тут мы используем стандарные свойства сравнения по модулю:

1) Если числа x и y сравнимы по модулю m, то их степени $x^n$ и $y^n$ тоже сравнимы по модулю m при любом натуральном n.

2) Если $a \equiv b$ $mod$ $m$, $x \equiv y$ $mod$ $m$, тогда $(a+x) \equiv (b+y)$ $mod$ $m$

3) Транзитивность: если $x \equiv y$ $mod$ $m$, $y \equiv z$ $mod$ $m$, тогда $x \equiv z$ $mod$ $m$

Вообще говоря, можно действовать без сравнений. Точнее использовать всю эту теорию в неявном виде. А именно:

Пусть перед нами натуральное число n. По условию при делении на 5 оно дает в остатке 4. То есть $(n-4) = 5k$, где $k$ - некотрое целое число. Перепишем равенство в виде $n = 5k+4$. Теперь возведем n в куб и квадрат:

$n^3 = (5k+4)^3 = 125k^3+300k^2+240k+64\\n^2 = (5k+4)^2 = 25k^2+40k+16$

Посчитаем сумму куба и квадрата нашего числа n:$n^3+n^2 = 125k^3+300k^2+240k+64 + 25k^2+40k+16 = 125k^3+325k^2+280k+80$

Убедимся, что эта сумма делится на 5. Для этого просто вынесем 5 за скобку:

$n^3+n^2 = 125k^3+325k^2+280k+80 = 5*(25k^3+65k^2+56k+16)$

Правая часть равенства, очевидно, делится на 5. Тогда и левая часть тоже делится на 5 (это следует из свойств делимости), то есть $(n^3+n^2)$ делится на 5. Что и требовалось доказать.

Однако следует заметить, что этот способ очень громоздкий. Посчитать куб и квадрат еще можно. А если степени большие, то счет становится очень длинным и долгим. Если степень "одноэтажная", может помочь бином, хотя с ним тоже не особо быстро всё получается посчитать. А если степени многоэтажные (как это часто бывает в стандартных задачках), то тут уже считать степени руками -- это абсурд. В таких задачах нужно использовать знания в области классов вычетов и сравений по модулю.