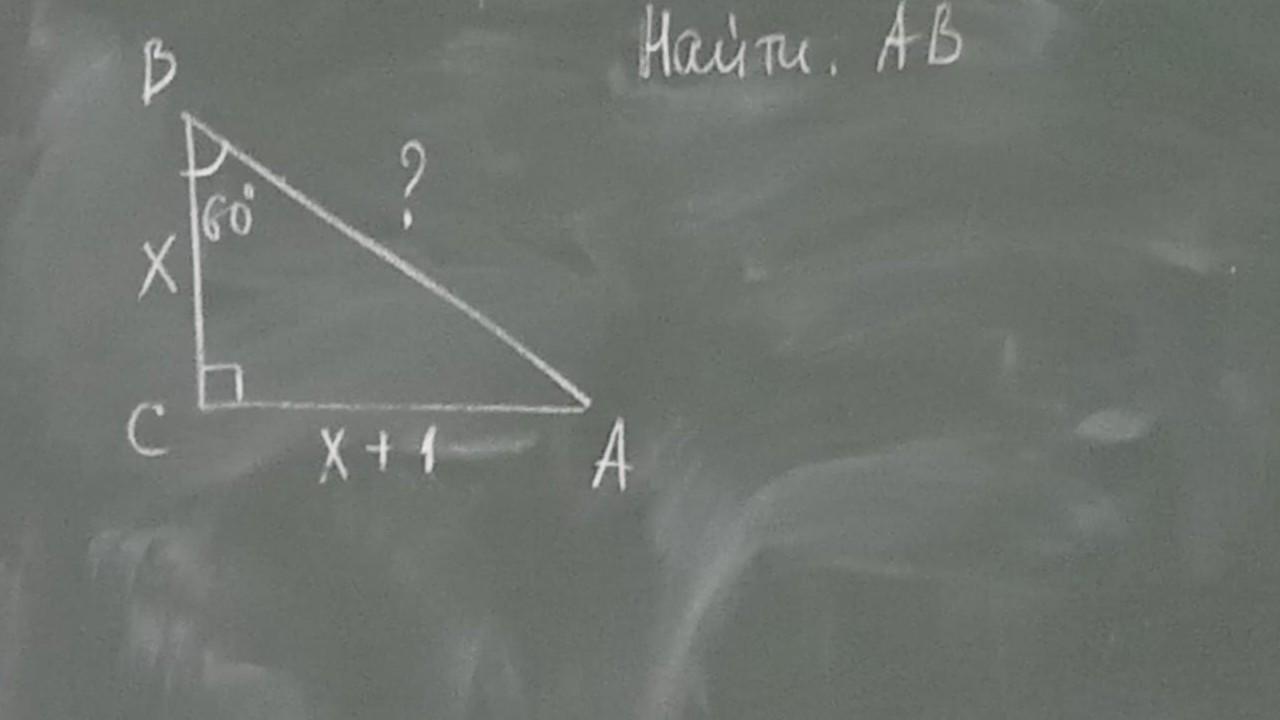Ответы
Ответ дал:
1
Ответ:
Объяснение:
Тангенс угла (tg α) - отношение противолежащего катета к прилежащему.
По теореме Пифагора:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад