В двух вершинах равностороннего треугольника со стороной 12 см находятся заряды -22 нКл и -25 нКл. Определить силу (мкН), действующую со стороны этих зарядов на заряд -12 нКл, находящийся в третьей вершине. Система зарядов находится в диэлектрике проницаемостью 5.4
Ответы
Ответ дал:
0
Ответ:
Объяснение:
Дано:
0,12 м
Кл
Кл
Кл
5,4
((H · м²)/(Кл²))
Найти:
------------------------------------------------
Решение:
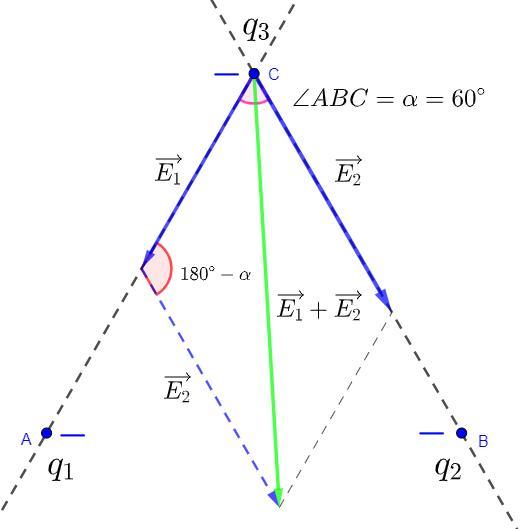
- напряженность электрического поля в точке
- сила электрического заряда
Кл *
/ (29,16 * 0,00020736 ((м²)²))) *
* ( Кл² +
Кл² + 2 *
Кл² * cos 60°) =
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад