Question

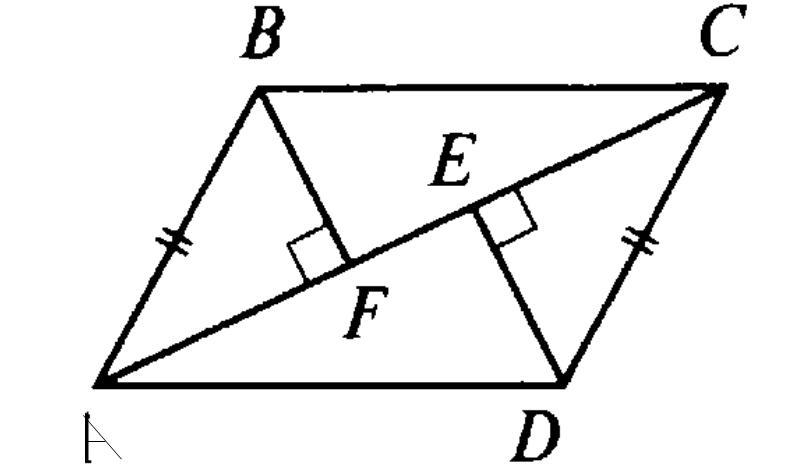
Известно, что АВ параллельно CD. Докажите, что BF=DE.
(Вспомните теоремы об углах, образованных двумя параллельными прямыми и секущей)

Answer 1

В четырёхугольнике ABCD AB II CD. AB=CD. AC - диагональ. BF⟂AC, ED⟂AC.

AC - диагональ. BF⟂AC, ED⟂AC.Докажите, что BF=DE.

Объяснение:

Рассмотрим прямоугольные треугольники ABF(∠F=90°) и △CDE(∠E=90°).

∠BAC=∠DCA - как внутренние накрест лежащие углы при параллельных прямых AB и CD и секущей AC.

AB=CD - по условию.

△ABF=△CDE по гипотенузе и острому углу.

• Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Из равенства треугольников следует равенство соответственных сторон: BF=DE, что и требовалось доказать.