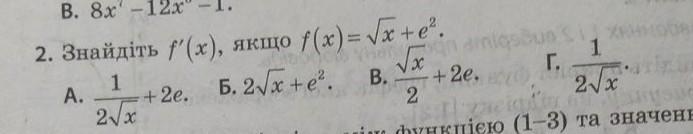Question

Розв'язати срочно...........100 балов​

Answer 1

$\displaystyle\bf\\f(x)=\sqrt{x} +e^{2} \\\\\\f'(x)=(\sqrt{x} +e^{2})'=(\sqrt{x})'+(e^{2} )'=\frac{1}{2\sqrt{x} } +0=\frac{1}{2\sqrt{x} }$

Ответ : Г

Answer 2

Ответ:

Г)1/(2√х)

Объяснение:

на самом деле в этом коротком примере много правил. см. ниже.

(√u)'=1/(2√u)*u'; (const)'=0; е²- это число, т.е. константа. х'=1

производная суммы равна сумме производных. поэтому

f'(х)=(√x+е²)'=(1/(2√х))*х'+0=1/(2√х)