Ответы
Ответ дал:
0
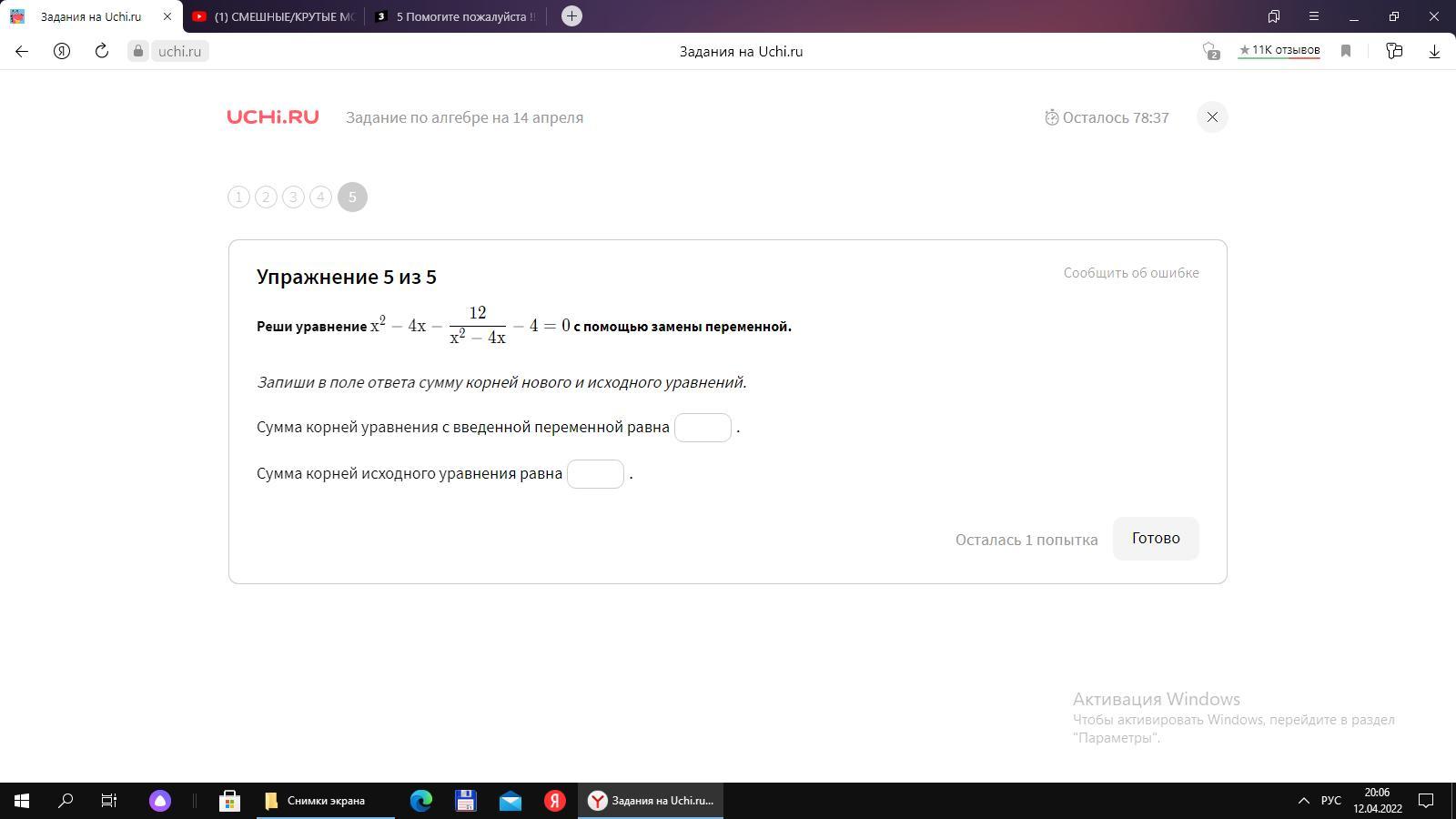
Сумма корней с введённой переменной равна :
Сумма корней исходного уравнения равна :
Сумма корней нового и исходного уравнений равна :
4 + 8 = 12
Ответ : 12
123452622:
а куда писать 12 ?
В поле ответа
так там два поле ответа первый для корней с введённой переменной где ты написал(а) 4 и еще есть Сумма корней исходного уравнения которая равна 8 а других полей для вода нету
ау
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад