Задана сфера, площадь которой равна 576Π см2. На сфере расположена точка A, через которую проведена касательная плоскость к сфере. В данной плоскости отмечена точка B. Кратчайшее расстояние от точки B до точки сферы равно 1 см. Найдите длину отрезка AB.
Ответы
Ответ дал:
7
Ответ:
AB=5см
Объяснение:
Площадь поверхности сферы радиуса r равна 4πr²=576π
значит r²=576/4=144
r=12см
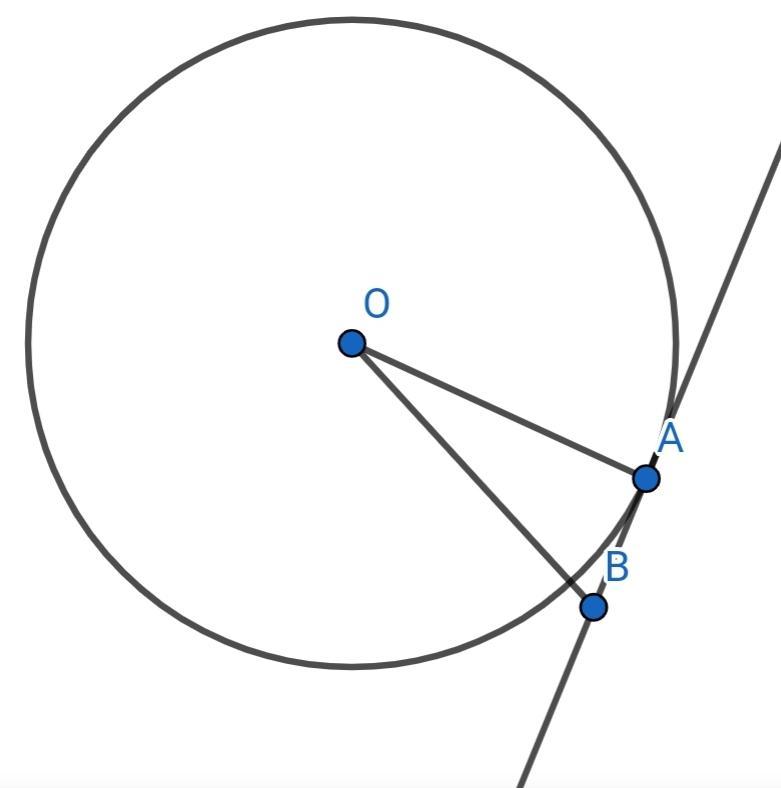
Заметим, что кратчайшее расстояние от точки вне сферы до поверхности сферы достигается на отрезке, соединяющем эту точку с центром сферы, значит, если O - центр сферы, то точки B и O лежат на одной прямой - значит в прямоугольном треугольнике AOB OA=12, OB=13см (13= радиус 12см + расстояние от B до сферы в 1 см), соответственно по теореме Пифагора AB²=13²-12²=169-144=25=5²
AB=5см
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад