Question

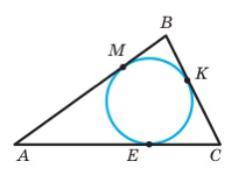
Коло, вписане в трикутник АВС, дотикається до його сторін в точках М, К, Е. Периметр трикутника АВС дорівнює 120. Знайдіть АМ, якщо ВК=12, КС=17.

Answer 1

Ответ:

АМ=31

Объяснение:

сторони трикутника – є дотичними до кола. Відрізки дотичних, проведені з однієї вершинии рівні між собою від вершини до точки дотику. Тому

МВ=ВК=12; КС=ЕС=17; АМ=АЕ

Нехай АМ=АЕ=х

ВС=ВК+КС=12+17=29.

Периметр – це сума усіх сторін трикутника.

Знаючи периметр, складемо рівняння:

АМ+МВ+ВС+ЕС+АЕ=120

х+12+29+17+х=120

2х+29+29=120

2х+58=120

2х=120–58

2х=62

х=62÷2

х=31 – це відрізки АМ=АЕ