Вычислить неопределённые интегралы
1. log xsin 3x dx
2. log xe^3x^2 dx
3. log x^2 / 1+ x^3 dx
Помогите, пожалуйста...
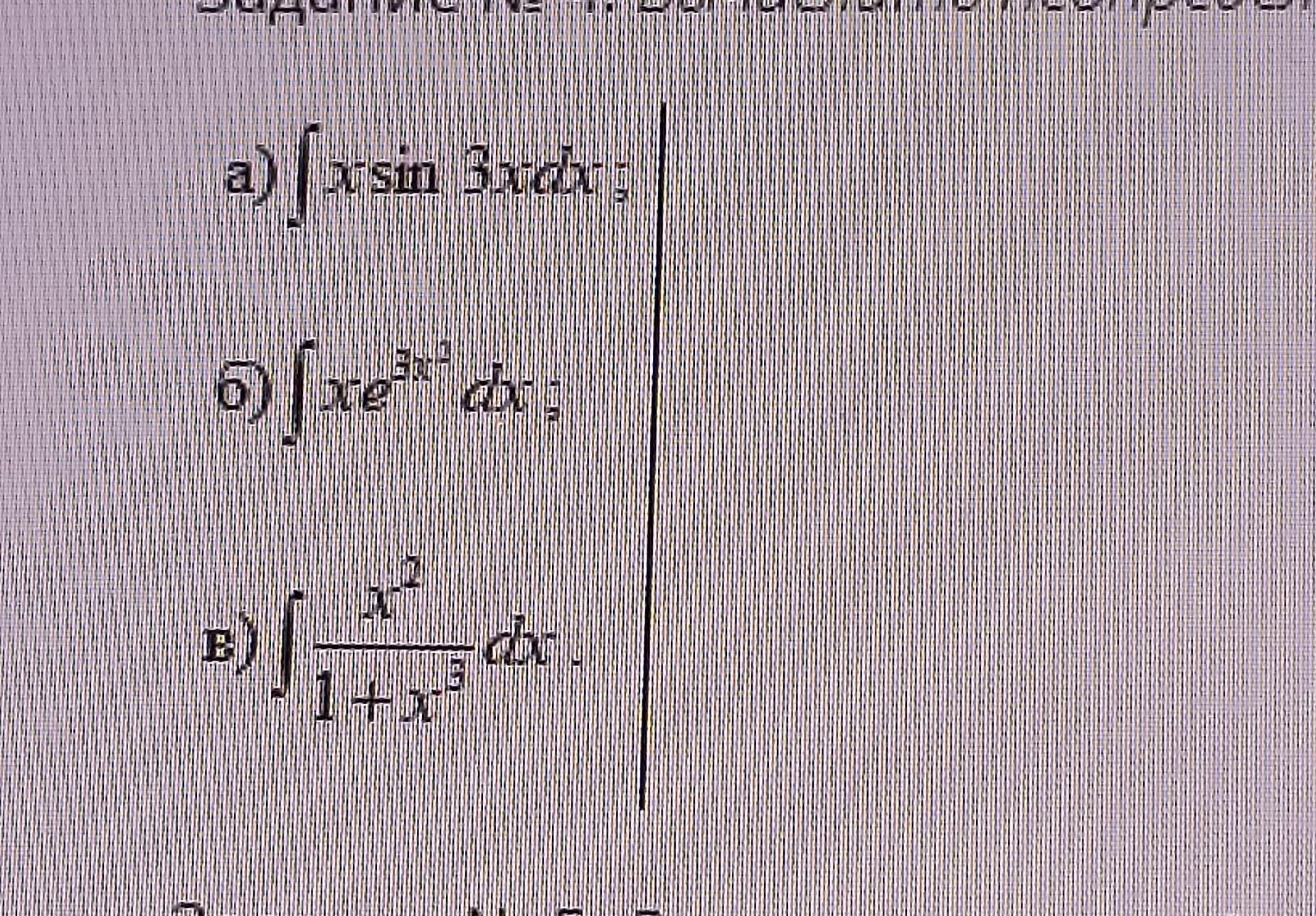
Ответы
Ответ:
1) Интегрирование по частям.
2) Подведение под знак дифференциала ( можно заменой).
3) Подведение под знак дифференциала ( можно заменой).
P.S. Если решать с помощью замены, то функцию, которую выделили под знаком дифференциала, заменять на новую переменную. Во 2 примере - это , в 3 примере - это
.
методом интегрирования по частям по формуле
∫udv=uv-∫vdu найдем
а) ∫х*sin3x{ x=u⇒dx=du;sin3xdx=dv⇒∫sin3xdx=∫dv⇒-cos3x/3=v}=
-(x*cos3x)/3-(1/3)∫(-cox3xdx)=-(x*cos3x)/3+(1/9)sin3x+c;
для б) в) используем метод подведения под знак дифференциала.
xdx=0.5d(x²)=0.5*(1/3)3d(3x²)=(1/6)d(3x²);
∫хе³ˣ²dx=∫(1/6)е³ˣ²d(3x²);=∫(1/6)e³ˣ²d(3x²)=(1/6)e³ˣ²+c;
в) ∫(х²/(1+х³)dx=(1/3)∫3x²dx/(1+x³)=(1/3)∫dx³/(1+x³)=(1/3)∫d(x³+1)/(1+x³)=
{табличный интеграл ∫du/u=㏑IuI+c}=㏑Ix³+1I+c