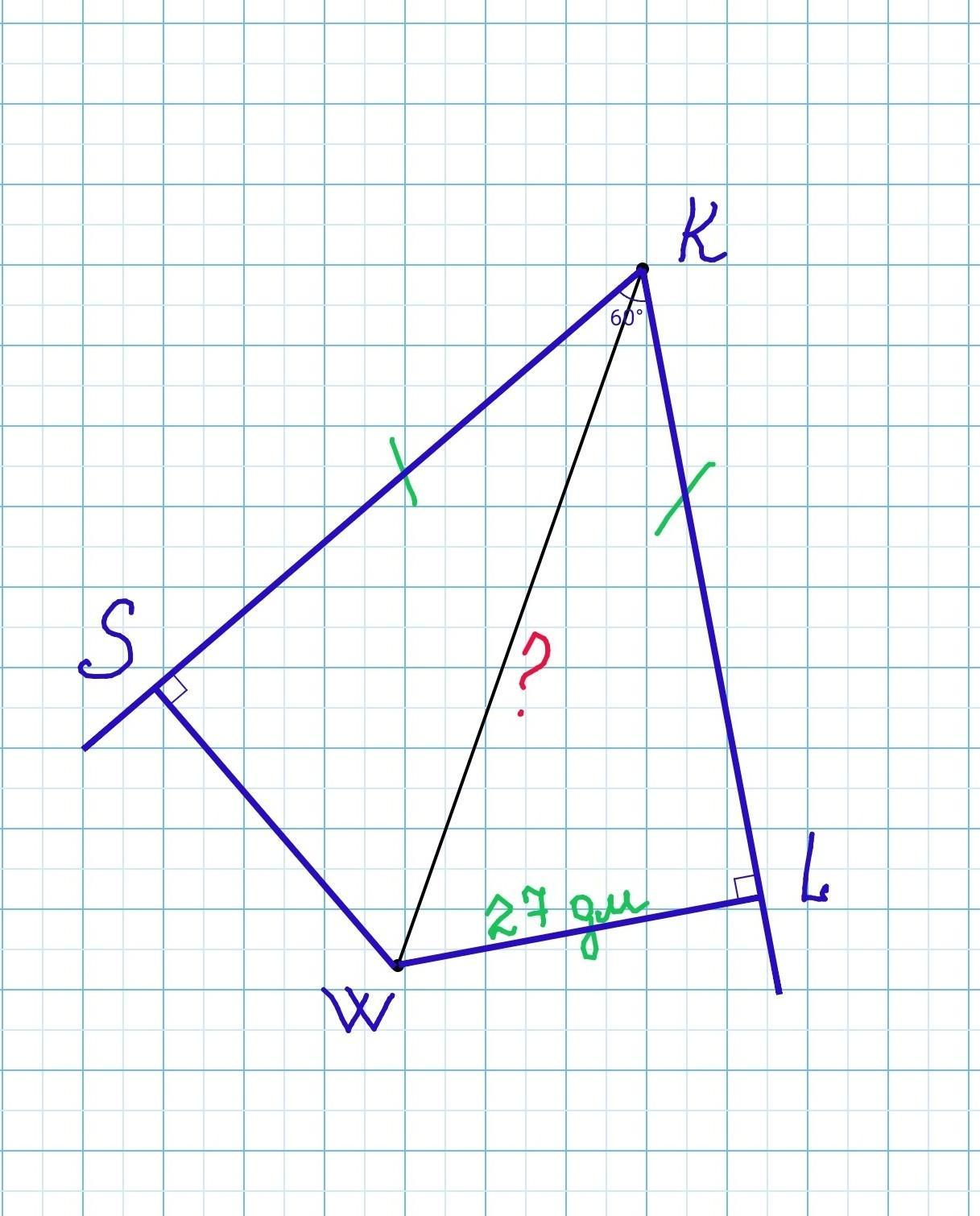
Луч KW провели так, что его начало совпадает с вершиной угла SKL , а расстояние от точки W до сторон KS и KL одинаковое. Найди KW , если SKL = 60 ∠SKL=60° , а LW=27 дм.
drmatykhin:
ответ в ДМ*
KW=2*LW=2*27=....... дм
Ответы
Ответ дал:
2
Ответ:
KW=54 дм
Объяснение:
Дан ∠SKL=60°. Из вершины К провели луч KW. Из точки W, принадлежащей лучу KW проведём перпендикуляры к сторонам ∠SKL: WS⟂KS, WL⟂KL.
Известно, что KS=KL, а LW=27 дм
Найдём KW.
Рассмотрим прямоугольные треугольники KSW(∠S=90°) и KLW(∠L=90°).
KS=KL - по условию, KW - общая.
Следовательно △KSW=△KLW по гипотенузе и катету.
Из равенства треугольников следует равенство углов:
∠SKW=∠LKW=∠SKL:2=60°:2=30°.
- В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
В прямоугольном треугольнике KLW катет LW лежит напротив ∠LKW=30°.
Гипотенуза KW=2•LW=2•27=54 дм
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад