Question

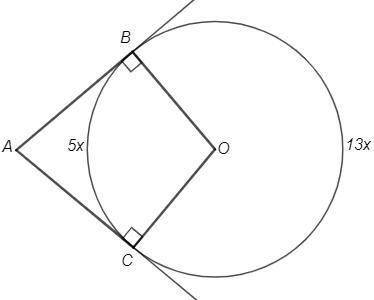
Из точки О проведены две касательные к окружности. Найдите угол между касательными, если эти касательные делят дугу окружности в отношении 13:5.​

Answer 1

Радиус в точку касания перпендикулярен касательной.

∠OBA=∠OCA=90°

В четырехугольнике ABOC сумма противоположных углов 180°, следовательно сумма двух других углов также 180°.

∠BOC+∠A =180°

Центральный угол равен дуге, на которую опирается.

∠BOC=◡BC

По условию точки касания делят окружность (360°) на дуги 5x и 13x

5x+13x =360° => x=20°

Понятно, что угол BOC опирается на меньшую дугу, так как он меньше 180°.

∠BOC =5x =100°

∠A =180°-∠BOC =80°