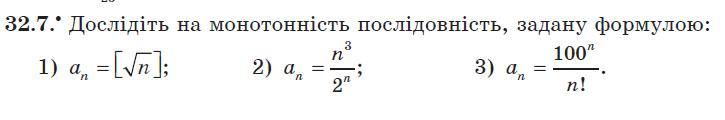Question

Задание приложено...

Answer 1

Ответ:

1) Монотонна

2) Монотонна

3) Не является монотонной

Примечание:

Тут и далее речь идет только о числовых последовательностях область определений которых является множество $\mathbb N$.

По определению монотонными последовательностями называют:

• Неубывающие
• Невозрастающие
• Убывающие
• Возрастающие

По определению:

Числовую последовательность $(a_{n})$ называют возрастающей, если для любого $n \in \mathbb N$ выполняется неравенство $a_{n} < a_{n + 1}$.

(Определение через кванторы: $\forall n \in \mathbb N : a_{n} < a_{n + 1}$)

Числовую последовательность $(a_{n})$ называют убывающей, если для любого $n \in \mathbb N$ выполняется неравенство $a_{n} > a_{n + 1}$.

(Определение через кванторы: $\forall n \in \mathbb N : a_{n} > a_{n + 1}$)

Числовую последовательность $(a_{n})$ называют невозрастающей, если для любого $n \in \mathbb N$ выполняется неравенство $a_{n} \geq a_{n + 1}$.

(Определение через кванторы: $\forall n \in \mathbb N : a_{n} \geq a_{n + 1}$)

Числовую последовательность $(a_{n})$ называют неубывающей, если для любого $n \in \mathbb N$ выполняется неравенство $a_{n} \leq a_{n + 1}$.

(Определение через кванторы: $\forall n \in \mathbb N : a_{n} \leq a_{n + 1}$)

Таким образом, если последовательность $a_{n}$ не относится ко всем выше перечисленным последовательностям, то она не является монотонной.

Объяснение:

32.7

1) $a_{n} = \sqrt{n}$

Рассмотрим несколько первых элементов последовательности:

$n = 1:a_{1} = [\sqrt{1} ] = 1$

$n = 2:a_{2} = [\sqrt{2} ] = 1$

$n = 3:a_{3} = [\sqrt{3} ] = 1$

$n = 4:a_{4} = [\sqrt{4} ] = 2$

$n = 5:a_{5} = [\sqrt{5} ] = 2$

Можем сделать гипотезу о том, что данная последовательность является неубывающей.

Рассмотрим $a_{n}$ и $a_{n + 1}$. Необходимо доказать, что $a_{n} \leq a_{n + 1}$.

$[\sqrt{n} ] \leq [\sqrt{n + 1} ]$

Если числи $\sqrt{n} , \sqrt{n + 1}$ лежат в промежутке от $[a;b]$, где $a,b -$ точные квадраты целых чисел, то выполняется равенство верно, а иначе $\sqrt{n} < \sqrt{n + 1}$  тоже верно, то есть $[\sqrt{n} ] \leq [\sqrt{n + 1} ]$ - верно, то есть последовательность является неубывающей, а следовательно монотонной.

2)

$a_{n} = \dfrac{n^{3}}{2^{n}}$

Рассмотрим несколько первых элементов последовательности:

$n = 1: a_{1} = \dfrac{1^{3}}{2^{1}} = \dfrac{1}{2} = 0,5$

$n = 2: a_{2} = \dfrac{2^{3}}{2^{2}} = 2^{3 - 2} = 2^{1} = 2$

$n = 3: a_{3} = \dfrac{3^{3}}{2^{3}} = \dfrac{27}{8} = 3,375$

Можем сделать гипотезу о том, что данная последовательность является возрастающей.

Рассмотрим $a_{n}$ и $a_{n + 1}$. Необходимо доказать, что $a_{n} < a_{n + 1}$.

$\dfrac{(n + 1)^{3}}{2^{n + 1}} > \dfrac{n^{3}}{2^{n}}$

$\dfrac{(n + 1)^{3}}{2^{n} \cdot 2^{1}} > \dfrac{n^{3}}{2^{n}} \bigg | \cdot \dfrac{2^{n}}{2}$

$(n + 1)^{3} > 2n^{3}$

$\sqrt[3]{(n + 1)^{3} } > \sqrt[3]{2n^{3}}$

$n + 1 > n\sqrt[3]{2}$

$n -n\sqrt[3]{2} > -1$

$n(1 -\sqrt[3]{2}) > -1|: (1 -\sqrt[3]{2})$

$n > \dfrac{-1}{(1 -\sqrt[3]{2})}$

$n > \dfrac{1}{\sqrt[3]{2} - 1}$

$\sqrt[3]{2} - 1 \lor 0$

$\sqrt[3]{2} \lor 1$

$(\sqrt[3]{2})^{3} \lor 1^{3}$

$2 > 1 \Longrightarrow \boxed{\sqrt[3]{2} - 1 > 0}$

-----------------------------------

$\dfrac{1}{\sqrt[3]{2} - 1} \lor 1| \cdot ({\sqrt[3]{2} - 1)$

$({\sqrt[3]{2} - 1) \lor 1|+1$

$\sqrt[3]{2} \lor 2$

$(\sqrt[3]{2})^{3} \lor 2^{3}$

$2 < 8 \Longrightarrow \boxed{\dfrac{1}{\sqrt[3]{2} - 1} < 1}$

А минимальное $n = 1$, то есть доказано, что $\dfrac{(n + 1)^{3}}{2^{n + 1}} > \dfrac{n^{3}}{2^{n}}$, то есть последовательность является возрастающей и следовательно

монотонной.

3)

$a_{n} = \dfrac{100^{n}}{n!}$

Можно предположить, что $100^{n}\gg n!$ и на основании данной гипотезы

сделать вывод, что последовательность является возрастающей.

Рассмотрим $a_{n}$ и $a_{n + 1}$. Необходимо доказать, что $a_{n} < a_{n + 1}$.

$\dfrac{100^{n + 1}}{(n + 1)!} > \dfrac{100^{n}}{n!}$

$\dfrac{100^{n} \cdot 100}{n! \cdot (n + 1)} > \dfrac{100^{n}}{n!} \bigg | \cdot \dfrac{n!}{100^{n}}$

$\dfrac{100}{n + 1} > 1 | \cdot (n + 1)$

$100 > n + 1$

$99 > n$

То есть гипотеза оказалась не верной и для всех $n$ последовательность не является возрастающей, в то же время в точке 100 последовательность меняет знак, а так как знак меняется или же неравенство верно для конечного множества из $n$ элементов, а не для все $n \in \mathbb N$, то можно сделать вывод, что данная последовательность не является монотонной.