Question

Помогите с математикой, и полное решение пожалуйста

Answer 1

Ответ:

$\LARGE \text{ \boxed{ \boldsymbol{ V = 60} }}$ кубических единиц

Объем второй пирамиды равен 60 кубических единиц

Пошаговое объяснение:

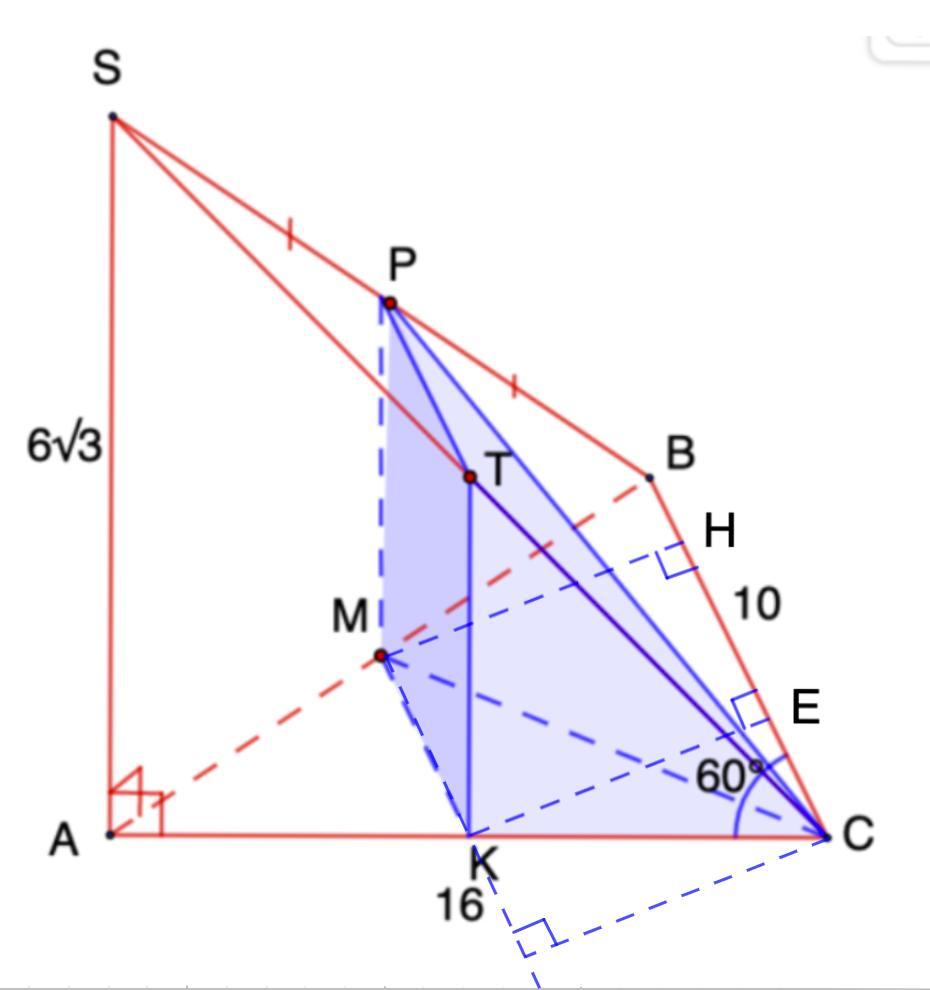
Дано: SABC - пирамида (S - вершина пирамиды), ∠ACB = 60°, AC = 16, BC = 10, SAC ⊥ ABC, SAB ⊥ ABC, SA = $6\sqrt{3}$, SM = MB

Построить: пирамиду с вершиной C основанием, которой является сечение пирамиды SABC плоскостью, проходящей через точку M параллельно прямым BC и AS

Найти: $V \ - \ ?$

План построения:

Через точку M проведем прямые параллельные SA и BC, пусть данные прямые пересекают отрезки AB и SC в точка K и T соответственно, то есть KM║AS, MT║BC.

Через точку K проведем прямую параллельную BC и пусть данная прямая пересекает AC в точке P, тогда по построению KP║BC.

По аксиоме стереометрии (аксиома прямой и плоскости) прямая, проходящая через две точки плоскости, лежит в этой плоскости, тогда:

• Так как M,K ∈ SAB, то MK ⊂ SAB
• Так как M,T ∈ SBC, то MT ⊂ SBC
• Так как K,C ∈ ABC, то KC ⊂ ABC
• Так как M,C ∈ SBC, то MC ⊂ SBC
• Так как K,P ∈ ABC, то KP ⊂ ABC

По теореме Фалеса:

• (угол ∠SBA) так как по условию BM = MS и KM║AS по построению, то BK = KA.

• (угол ∠BAC) так как BK = KA и KP║BC по построению, то

        AP = PC.

• (угол ∠SBC) так как по условию BM = MS и MT║BC по  построению, то ST = TC.

Так как MT║BC и PK║BC, то по свойству транзитивности параллельных прямых MT║PK.

Так как ST = TC и AP = PC, то по определению отрезок PT - средняя линия в треугольнике ΔSAC, тогда по свойствам средней линии она параллельна стороне треугольника с которой не имеет общих точек, то есть PT║SA.

Так как PT║SA и MK║SA, то по свойству транзитивности параллельных прямых PT║MK.

Так как PT║MK и MT║PK, то по определению четырехугольник

KMTP - параллелограмм.

По следствию из аксиом стереометрии через две параллельные прямые можно провести плоскость и притом только одну, тогда так как MT║PK, то данные прямые однозначно задают плоскость KMT (точка  P ∈ KMT).

По теореме если прямая, которая не принадлежит данной плоскости, параллельна какой-нибудь прямой, которая лежит в этой плоскости, то данная прямая параллельна самой плоскости, так как KP║BC по построению и BC ⊄ KMT, то BC║KMT, аналогично так как PT║AS и AS ⊄ KMT, то AS║KMT.

Тогда так как AS║KMT и BC║KMT, то сечение пирамиды SABC плоскостью, проходящей через точку M параллельно прямым BC и AS является четырехугольник KMTP.

Так как точка С ∉ MKT, то многогранник CKMTP - является фигурой требуемой по построению, то есть пирамидой.

Решение:

По аксиоме стереометрии (аксиома пересечения плоскостей) если две плоскости имеют общую точку то их пересечение есть прямая,

тогда по следствию из данной аксиомы:

• Так как A ∈ SAB,SAC и S ∈ SAB,SAC ,то SAB ∩ SAC = SA

По теореме если каждая из двух плоскостей, которые пересекаются  перпендикулярна к третьей плоскости, то прямая их пересечения перпендикулярна к этой плоскости, так как SAB ∩ SAC = SA и по условию SAC ⊥ ABC, SAB ⊥ ABC, тогда SA ⊥ ABC.

Из точки C проведем перпендикуляр к прямой PK в точку H, то есть  CH ⊥ PK, следовательно треугольник ΔHPC - прямоугольный.

По аксиоме стереометрии (аксиома прямой и плоскости) прямая, проходящая через две точки плоскости, лежит в этой плоскости, тогда так как по построению H ∈ PK и PK ⊂ ABC, то H ∈ ABC, а также C ∈ ABC, следовательно HC ⊂ ABC.

По теореме если одна из двух параллельных прямых перпендикулярна данной плоскости, то и вторая прямая перпендикулярна этой плоскости, тогда так как PT║SA и SA ⊥ ABC, то PT ⊥ ABC.

По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как SA ⊥ ABC и HC ⊂ ABC, то SA ⊥ HC, аналогично так как PT ⊥ ABC и PK ⊂ ABC, то PT ⊥ PK.

По теореме (признак перпендикулярности прямой и плоскости) если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то оно перпендикулярна этой плоскости, тогда так как CH ⊥ PT и по построению CH ⊥ PK, то CH ⊥ KPT.

Рассмотрим параллелограмм PTMK. По теореме если один из углов параллелограмма прямой, то этот параллелограмм - прямоугольник, так как TP ⊥ KP и PTMK - параллелограмм, то PTMK - прямоугольник.

Так как BK = KA и AP = PC, то по определению отрезок PK - средняя линия в треугольнике ΔABC, тогда по определению средней линии

AP = PC.

По свойствам средней линии она равна половине стороны треугольника с которой не имеет общих точек, тогда так как PK - средняя линия в треугольнике ΔABC (PK║BC), то

PK = BC : 2 = 10 : 2 = 5, аналогично PT - средняя линия в треугольнике ΔSAC (PT║SA), то PT = SA : 2 = $6\sqrt{3} : 2 = 3\sqrt{3}$.

Так как по основному свойству отрезка AC = AP + PC и AP = PC, то AP = PC = AC : 2 = 16 : 2 = 8.

Так как PTMK - прямоугольник, то по формуле площади прямоугольника: $\boldsymbol{ S_{PTMK}} = KP \cdot TP = 5 \cdot 3\sqrt{3} = \boldsymbol{ 15\sqrt{3} }$ квадратных единиц.

По теореме угол ∠ACB = ∠CPH = 60° как внутренние накрест лежащие углы при параллельных прямых и секущей, так как PK║BC и AC - секущая.

Продолжение решения смотрите на фотографии!!!

Answer 2

Ответ:

Объем второй пирамиды равен 60 ед.²

Пошаговое объяснение:

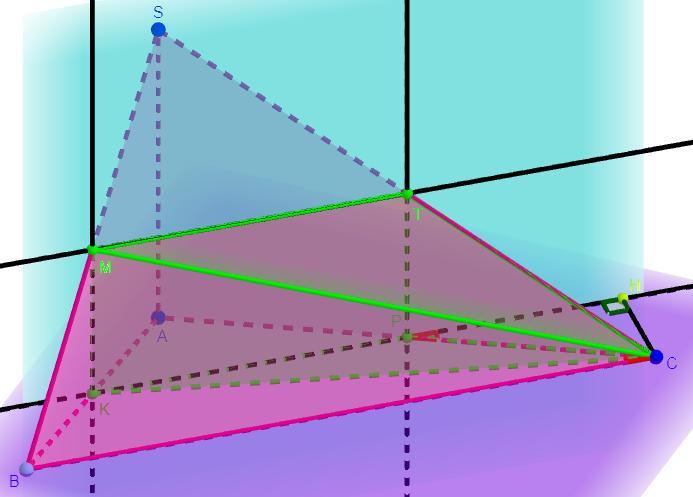
В основании пирамиды SАВС лежит треугольник АВС, в котором угол С = 60º, АС = 16 , BC = 10. Боковые грани SAC и SAB перпендикулярны плоскости основания пирамиды, а ребро SА равно 6√3. Сечение пирамиды плоскостью, проходящей через середину ребра SB параллельно прямым ВС и АS, является основанием второй пирамиды, вершина которой в точке С.

Найдите объем второй пирамиды.

Дано: SАВС - пирамида;

ΔАВС - основание;

∠С = 60°; АС = 16; BC = 10; SА = 6√3.

ΔSAC ⊥ ΔАВС; ΔSAB ⊥ ΔАВС.

Р - середина SB;

Сечение МПТК, проходящее через точку Р, параллельно прямым ВС и АS.

МПТК - основание пирамиды СМПТК.

Найти: V (СМПТК)

Решение:

• Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

Построим сечение МПТК || ВС и АС.

PT || BC; MK || BC;

MP || AS; TK || AS

⇒ МПТК - параллелограмм;

AS ⊥ ΔABC ⇒ PM ⊥ ΔABC

⇒ МПТК - прямоугольник.

Объем пирамиды найдем по формуле:

$\displaystyle \boxed {V=\frac{1}{3}S_{OCH}\cdot{H} }$

1. Рассмотрим ΔASB.

• Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения есть перпендикуляр к этой плоскости.

⇒ ΔASB - прямоугольный.

SP = PB (условие)

МРТК || AS ⇒ MP || AS

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ МР - средняя линия ΔASB.

• Средняя линия равна половине длины стороны, которую она не пересекает.

⇒ МР = SA : 2 = 6√3 : 2 = 3√3.

2. Рассмотрим ΔCSB.

SP = PB (условие)

МРТК || BC ⇒ PT || BC

⇒ средняя линия ΔCSB.

PT = CB : 2 = 10 : 2 = 5

3. Найдем площадь МРТК - основания пирамиды СМПТК.

• Площадь прямоугольника равна произведению смежных сторон.

S (МРТК) = MP · PT = 3√3 · 5 = 15√3

4. Найдем сторону АВ из ΔАВС по теореме косинусов.

• Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

АВ² = АС² + ВС² - 2 · АС · ВС · cos60°

АВ² = 256 + 100 - 2 · 16 · 10 · 0,5 = 196

АВ = √196 = 14

АМ = МВ = 14 : 2 = 7 (МР - средняя линия)

5. Высота СМПТК будет равна высоте трапеции СКМВ, так как расстояния между двумя параллельными прямыми равны.

Проведем высоты МН и КЕ.

ЕКМН - прямоугольник.

⇒ МК = НЕ = 5

СЕ + НВ = 10 - 5 = 5

Пусть СЕ = х, тогда НВ = 5 - х; КЕ = МН = h

По теореме Пифагора:

из ΔКЕС:

h² = KC² - CE² = 64 - x²   (1)

из ΔМВН

h² = MB² - (5-x)² = 49 - 25 + 10x - x² = 24 + 10x - x²    (2)

Приравняем (1) и (2):

64 - x² = 24 + 10x - x²

10х = 40

х = 4

СЕ = 4,  НВ = 5 - 4 = 1

Тогда h² = 64 - 16 = 48

h = 4√3

6. Теперь найдем объем:

$\displaystyle V=\frac{1}{3}\cdot15\sqrt{3}\cdot4\sqrt{3}=60$

Объем второй пирамиды равен 60 ед.²