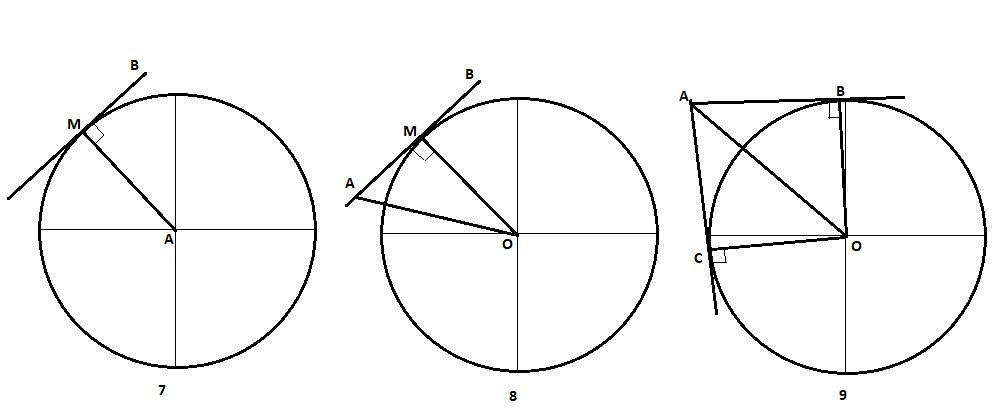Question

Решите пожалуйста!

7. АМ – радиус окружности с центром в точке А. Прямая АВ перпендикулярна прямой АМ.

Является ли АВ касательной к этой окружности

8. Определите вид треугольника АМО, если АВ – касательная к окружности с центром О, а

точка касания обозначена буквой М.

9. Сравните длины отрезков АВ и АС, если точка А не принадлежит некоторой окружности,

а АВ и АС две касательные к этой окружности ​

Answer 1

Ответ:

Ответы в Объяснении

Объяснение:

7. АМ – радиус окружности с центром в точке А. Прямая АВ перпендикулярна прямой АМ.

Является ли АВ касательной к этой окружности?

Ответ: да, потому что касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

8. Определите вид треугольника АМО, если АВ – касательная к окружности с центром О, а точка касания обозначена буквой М.

Ответ: Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, треугольник AMO - прямоугольный.

9. Сравните длины отрезков АВ и АС, если точка А не принадлежит некоторой окружности, а АВ и АС две касательные к этой окружности.

Ответ: AB = AC.

Два прямоугольных треугольника AOB и AOC равны друг другу, потому что у них катеты OB = OC = R, а гипотенуза AO - общая.