Ответы
Ответ дал:
0
Ответ:
20
Объяснение:
поскольку треугольник CDB прямоугольный, и катет DB вдвое меньше гипотенузы CB, то угол между ними будет 60 градусов(треугольник CDB как половинка равностороннего треугольника). Поскольку в треугольнике ACB(снова рассматриваем его как половинку равностороннего треугольника) катет CB=10 и угол между катетом и гипотенузой 60 градусов, тогда гипотенуза вдвое больше CB, то есть 20.
bot01:
а можно по другому
Ответ дал:
1
Ответ:
АD=15ед
Решение:
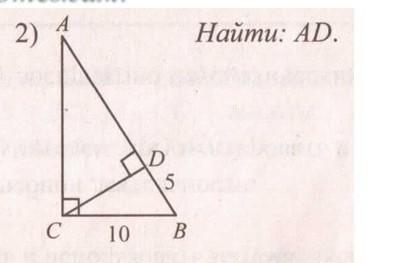
Пропорциональные отрезки прямоугольного треугольника:
СВ²=AB*DB;
AB=CB²/DB=10²/5=20ед.
AD=AB-BD=20-5=15ед.
____________
Решение 2)
∆СDB- прямоугольный треугольник.
DB=5; СВ=10. Катет больше гипотенузы в два раза, ∠DCB=30°; ∠B=60°;
∆АСВ- прямоугольный треугольник
∠B=60°; ∠A=30°
CB- катет против угла ∠А=30°
АВ=2*СВ=2*10=20ед.
АD=AB-BD=20-5=15ед.
АD=15ед
Решение:
Пропорциональные отрезки прямоугольного треугольника:
СВ²=AB*DB;
AB=CB²/DB=10²/5=20ед.
AD=AB-BD=20-5=15ед.
____________
Решение 2)
∆СDB- прямоугольный треугольник.
DB=5; СВ=10. Катет больше гипотенузы в два раза, ∠DCB=30°; ∠B=60°;
∆АСВ- прямоугольный треугольник
∠B=60°; ∠A=30°
CB- катет против угла ∠А=30°
АВ=2*СВ=2*10=20ед.
АD=AB-BD=20-5=15ед.
решите пожалуйста у меня еще в профиле
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад