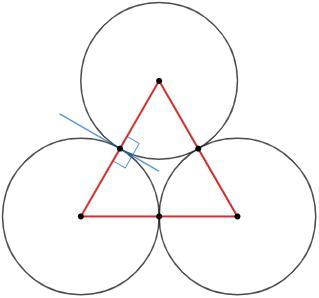
Три окружности одинакового радиуса попарно касаются друг друга. Докажите, что их центры являются вершинами пра- вильного треугольника.
Ответы
Ответ дал:
7
Ответ:
Точка касания двух окружностей лежит на линии центров. Расстояние между центрами равно сумме радиусов. И так для каждой пары окружностей. Каждая сторона треугольника равна двум радиусам. Треугольник равносторонний по определению.
Объяснение:
Касательная имеет с окружностью только одну общую точку. Остальные точки прямой удалены от центра более радиуса. Тогда радиус в точку касания - кратчайшее расстояние до прямой, т.е. перпендикуляр.
Две касающиеся окружности имеют общую касательную через точку касания. Радиусы в точку касания перпендикулярны касательной. Значит они образуют развернутый угол и лежат на одной прямой.
Приложения:
englerslavik34:
спасибоо
как сделать это лучшим ответом?
ХD
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад