Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
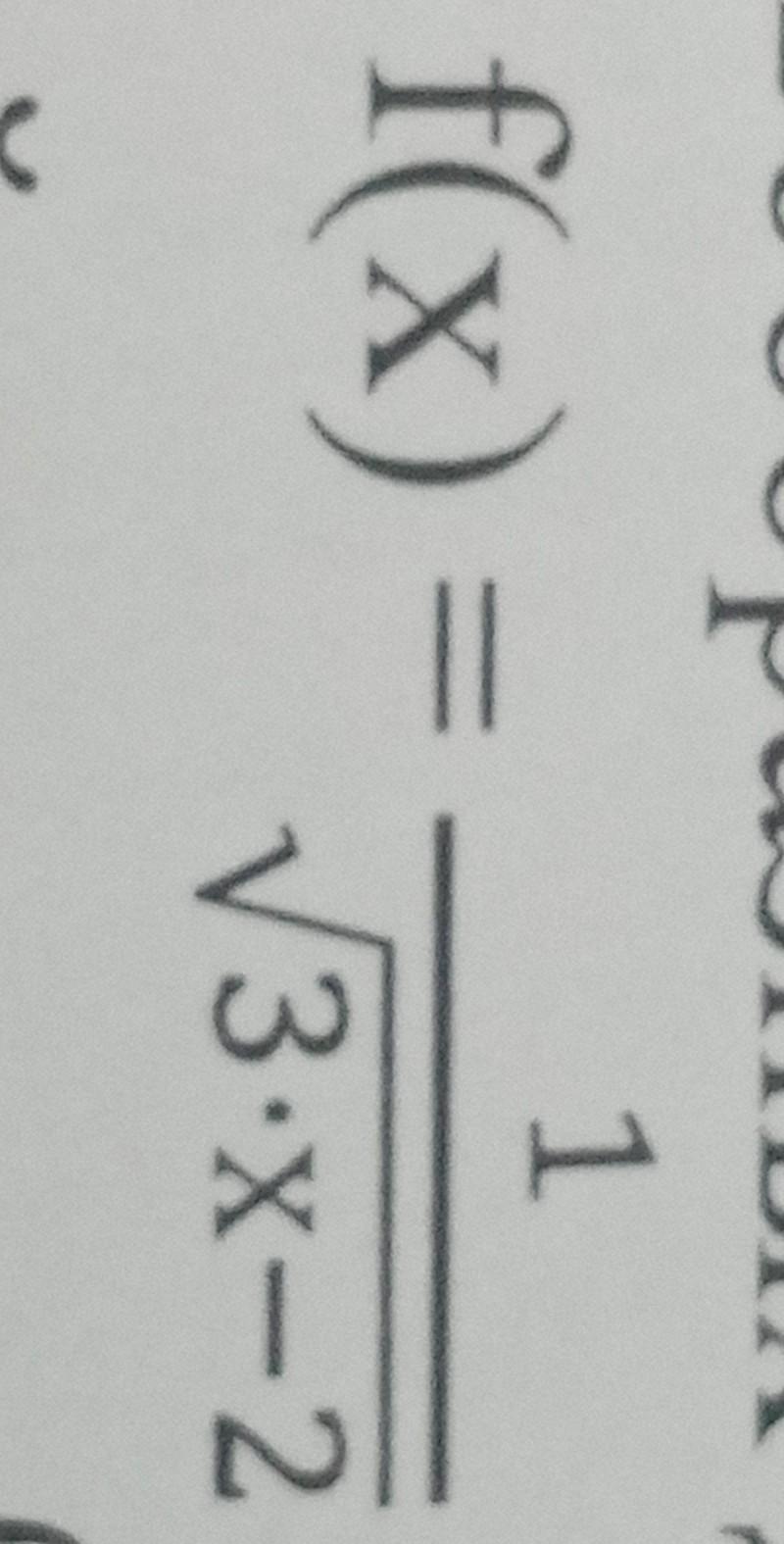
Задана функция:
Первообразная:
Произведем замену:
t = 3·x - 2
Тогда:
dt = 3·dx
Имеем:
Табличный интеграл:
И тогда, возвращаясь к прежней переменной:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад