Ответы
Ответ дал:
9
Ответ:
AB=2a/sin α
Объяснение:
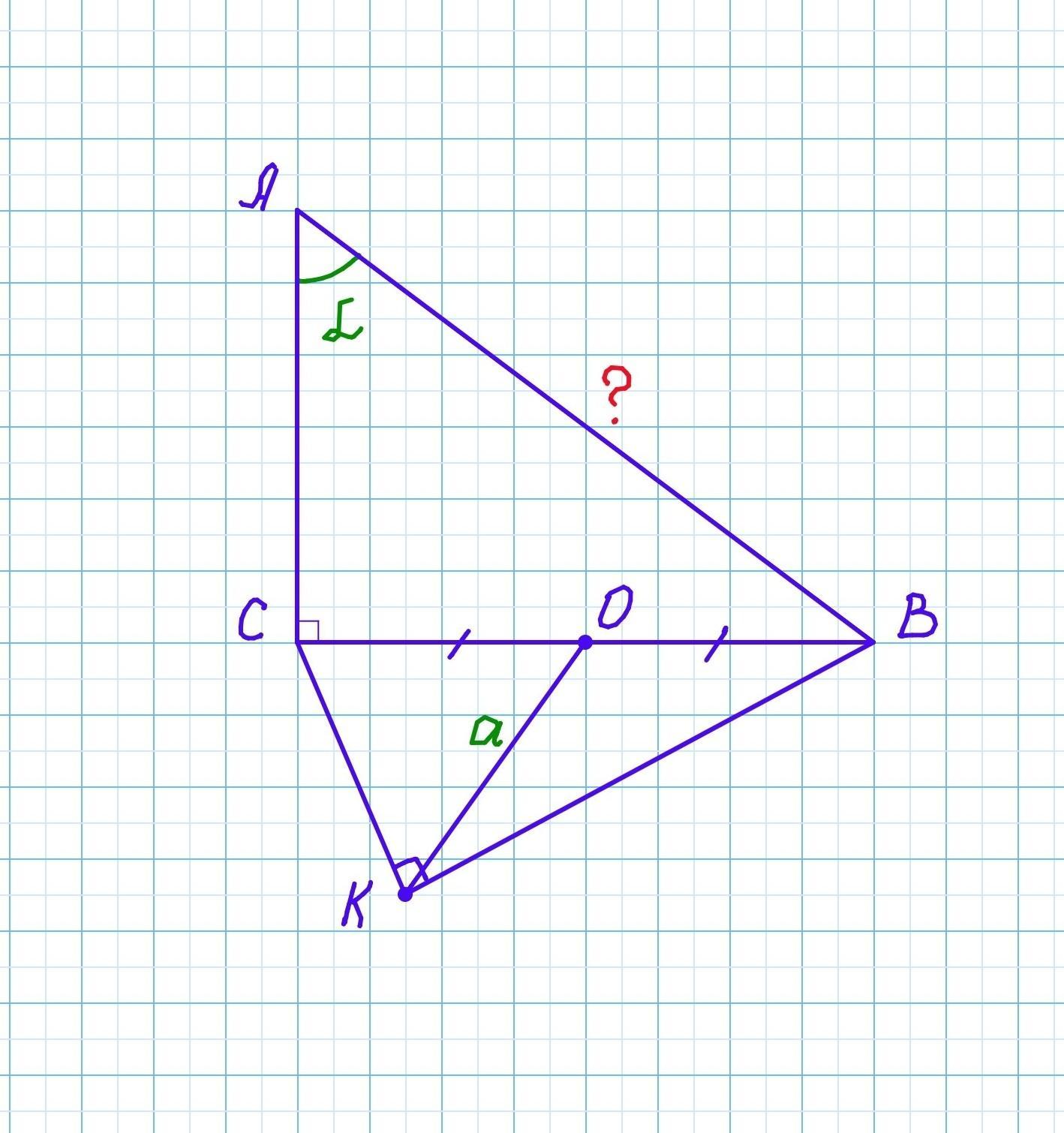
Дано: △ABC(∠C=90°), ∠A=α,
△BKC(∠BKC=90°), KO = a.
Найти: АВ.
1) Рассмотрим △BKC(∠BKC=90°).
- В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Так как CO=OB, KO - медиана, проведенная из вершины ∠BKC=90°.
Следовательно КО = ½•ВС.
ВС =2•КО=2а.
2) Рассмотрим △ABC(∠C=90°).
- Синус угла - это отношение противолежащего катета к гипотенузе.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад