Помогите ПЖ!!! Будь-який трикутник, сторони якого пропорційні числам 3, 4 і 5, — прямокутний. Знайдіть радіус і довжину кола описаного навколо трикутника зі сторонами 15 м, 20 м і 25 м
Ответы
Ответ дал:
1
Ответ:
Радиус описанной окружности равен 12,5м
Длина окружности равна 25π м
Объяснение:
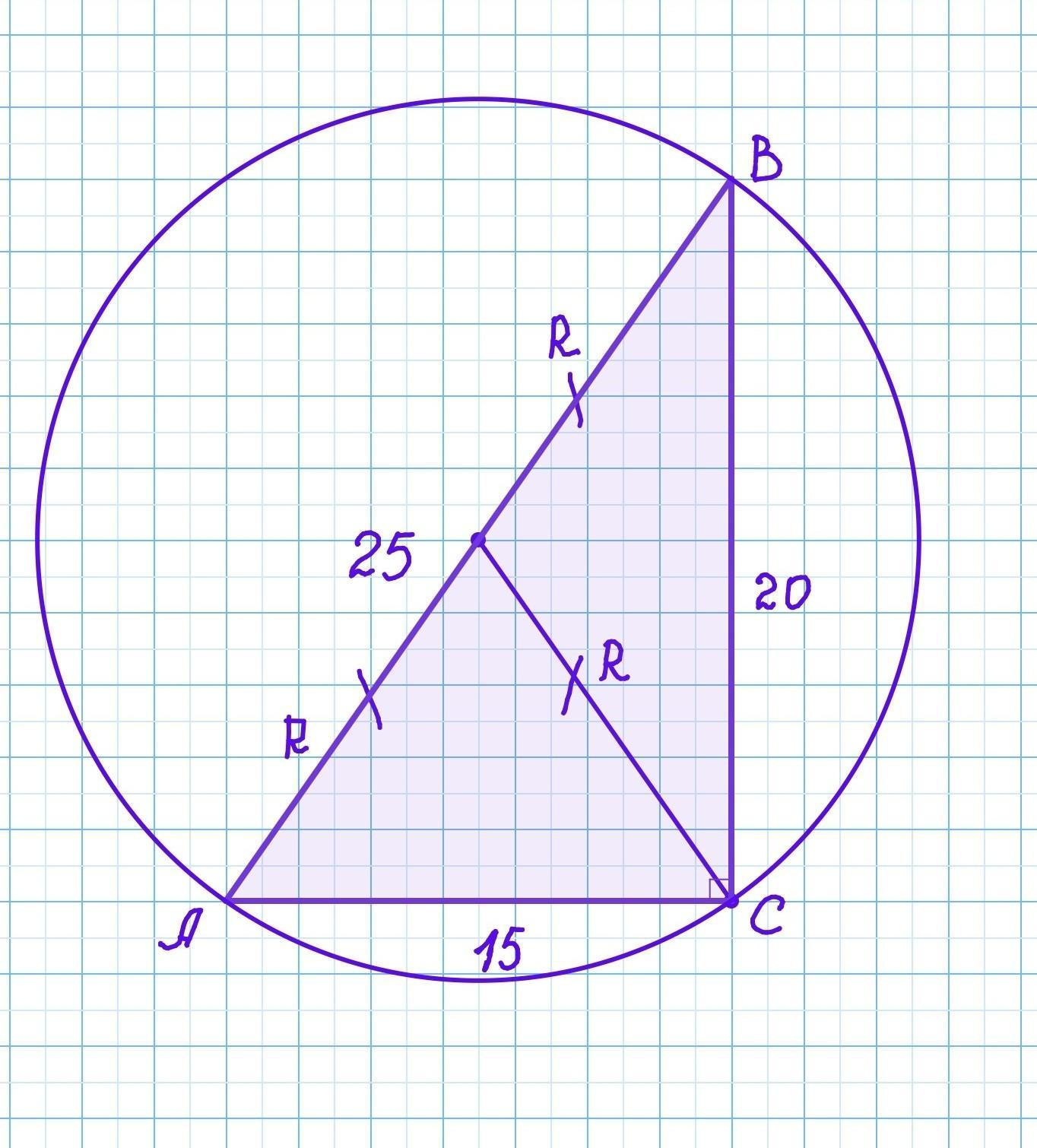
Так как 15:20:25=3:4:5, то есть стороны треугольника пропорциональны числам 3,4 и 5. Значит данный треугольник прямоугольный.
Действительно, согласно обратной теореме Пифагора: если квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон, то треугольник прямоугольный, имеем:
15²+20²=25²
225+400=625
625=625 - верно.
Следовательно АВ=25 - гипотенуза треугольника АВС.
- Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.
R=½•AB=½•25=12,5 м
- Длина окружности равна
м
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад