Ответы
Ответ дал:
1
Ответ:
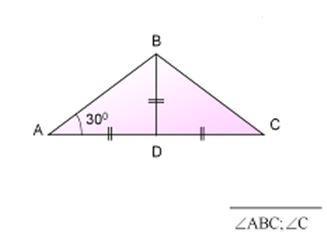
По рисунку видим что ΔАВД и ΔВДС равные, следовательно:
∠С=∠А=30°
∠АВС=2∠А=2*30=60°
Ответ дал:
1
Ответ:
∠C=60°; ∠ABC=90°
Решение:
∆АDB- равнобедренный треугольник.
В равнобедренном треугольнике углы при основании равны.
∠ВАD=∠ABD=30°
∠BDC- внешний угол треугольника ∆АВD; Внешний угол треугольника равен сумме двух внутренних углов треугольника не смежных с ним.
∠ВDC=∠BAD+∠ABD=30°+30°=
=60°.
∆BDC- равнобедренный треугольник.
В равнобедренном треугольнике углы при основании равны. (∠DBC=∠DCB)
Сумма углов в треугольнике равна 180°;
∠DCB=(180°-∠BDC)/2=
=(180°-60°)/2=60°.
∆DCB- равносторонний треугольник, все углы по 60°
∠АВС=∠АВD+∠DBC=30°+60°=90°
_________________
Медиана BD, равна половине гипотенузы. ∆АВС- прямоугольный треугольник; ∠АВС=90°.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад