Question

Основанием пирамиды с равными боковыми рёбрами является прямоугольник со стороной 6 и 8см боковое ребро пирамиды равно 6см найти высоту пирамиды
СРОЧНО НУЖНО РЕШЕНИЕ
РЕШИТЕ ПОЖАЛУЙСТА

Answer 1

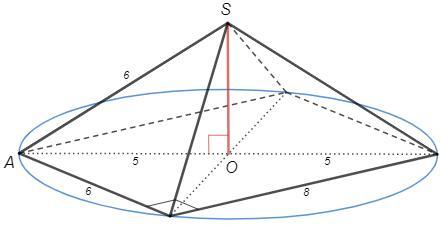
Опустим высоту пирамиды SO.

Соединим проекцию вершины пирамиды (O) с вершинами основания.

Получим равные прямоугольные треугольники (высота - общий катет, боковые ребра - равные гипотенузы).

Проекция вершины равноудалена от вершин основания, следовательно является центром описанной окружности основания.

Eсли в пирамиде боковые ребра равны, то вершина проецироется в центр описанной окружности основания.

В прямоугольнике центр описанной окружности - середина диагонали.

(Диагонали прямоугольника равны и точкой пересечения делятся пополам.)

т Пифагора

диагональ 10, радиус описанной окружности 5.

△SAO: SO =√(36-25) =√11 (см)