Помогите решить пожалуйста(высшая математика)
Вычислить предел (по правилу Лопиталя)
Приложения:
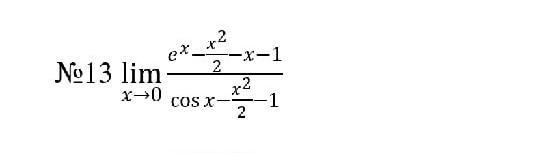
islamgaliajzere:
хочешь я скажу тебе где тебе можно найти ответ кроме брайнли?
где ?
на одном сайте
skysmart.com
вроде
а тут не как ?
никто не поможет
не хочешь не заходи на этот сайт
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Неопределеннось (0/0 )
Найдем производную от числителя и знаменателя дроби, стоящей под знаком предела:
Получили:
Опять неопредеденность (0/0).
Еще раз применим правило Лопиталя:
Окончательно:
Ответ: предел равен 0.
Спасибо!! а как найти 2 производную от этого ответа
:))) Вторая производная от ответа равна 0. Может, найти вторую производную от выражения, находящейся под знаком предела? :) Могу!
Было бы не плохо,спасибо за ответ ☺️
можно 2 производную пожалуйста
В комментах это невозможно (негде писать!), создай новое задание!
создал
как сможешь реши
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад