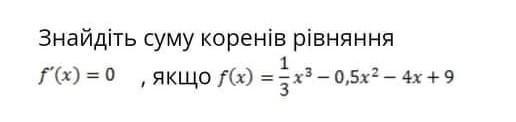Ответы
Ответ дал:
3
Найти сумму корней уравнения f'(x)=0, если f(x)=(1/3)x^3-0,5x^2-4х+9
Ответ:
Сумма корней уравнения 1.
Объяснение:
Правила нахождения производных, которые будут использоваться:
где х - переменная, с - постоянная.
Для начала найдём f'(x), тоесть производную функции:
Мы нашли f'(x), приравниваем выражение к нулю и решаем уравнение:
Это квадратное уравнение. Так как нам необходимо найти суму его корней, воспользуемся теоремой Виета. Но сначала убедимся, что корни есть (D≥0)
D=17≥0 - корни есть. Решаем по т. Виета.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад