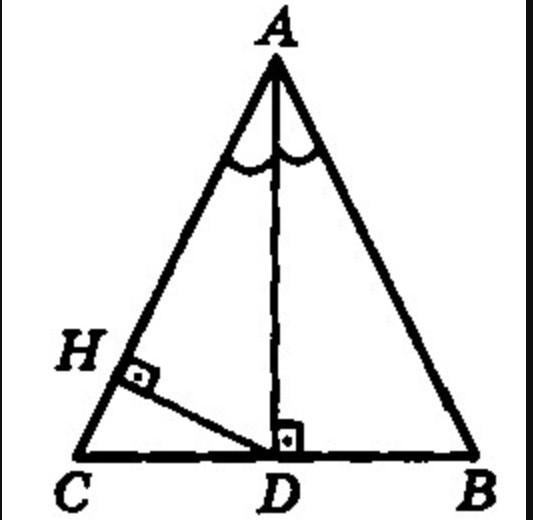
Дано: треугольник АВС — равносторонний, AD — биссектриса, DH — расстояние от точки D до АС, DH = 6 см. Найти: AD. 2. В треугольнике АВС угол С=30, АС=10 см, ВС=8см. Через вершину А проведена прямая а, параллельная ВС. Найдите расстояние от точки В до прямой АС.
Ответы
Ответ дал:
1
Ответ:
В равностороннем треугольнике все углы по 60°.
Тогда ∠DAH = 30° (H ∈ AC, DH ⊥ AC)
По условию DH=6см
В прямоугольном ΔADH HD - это катет, лежащий против угла в 30°. Тогда гипотенуза AD=2HD=12(см).
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад