Ответы
Ответ дал:
6
Ответ:
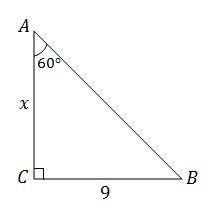
Дано: ΔАBC , ∠C прямой =90° ,∠А=60° , СB=9см
Найти: АС
Решение:
Сумма острых углов прямоугольного треугольника равна 90°.
Если прямой угол , тогда ∠
.
Катет АС лежит против угла , значит он равен половине гипотенузы AB.
Возьмём гипотенузу за 2х и составим уравнение -
по теореме Пифагора(квадрат гипотенузы равен сумме квадрата катетов).
Ответ: 
Приложения:
Ответ дал:
5
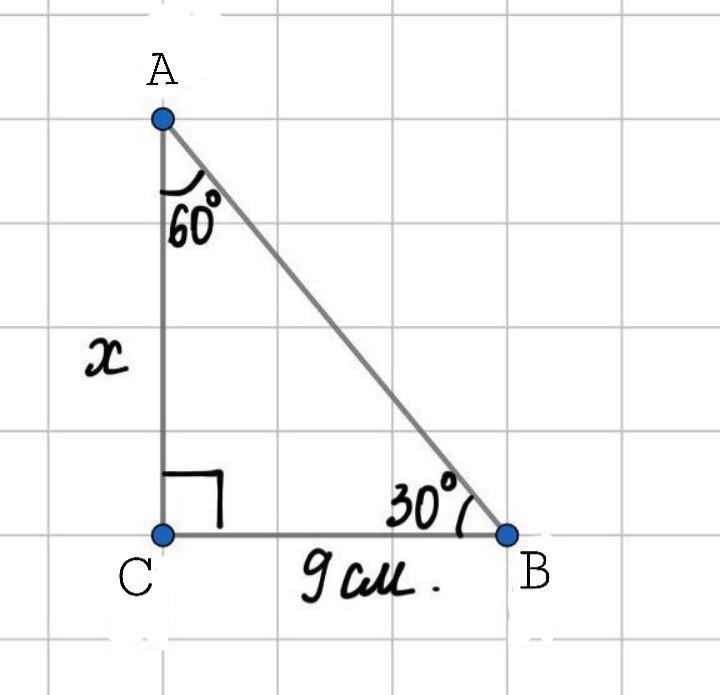
Дано:ΔАBC , ∠A = 60° ,∠C = 90°, катет CB равен 9см
Найти: катет AC
• Применим теорему синусов.Она у нас выглядит таким образом:
• Так как сумма острых углов прямоугольного треугольника равна 90°
• Чтобы найти катет применим теорему синусов.
• Против лежит катет
, а против
лежит катет
.
Следовательно:
• Пропорция.Умножаем накрест.
• В знаменателе избавимся от иррациональности.
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад