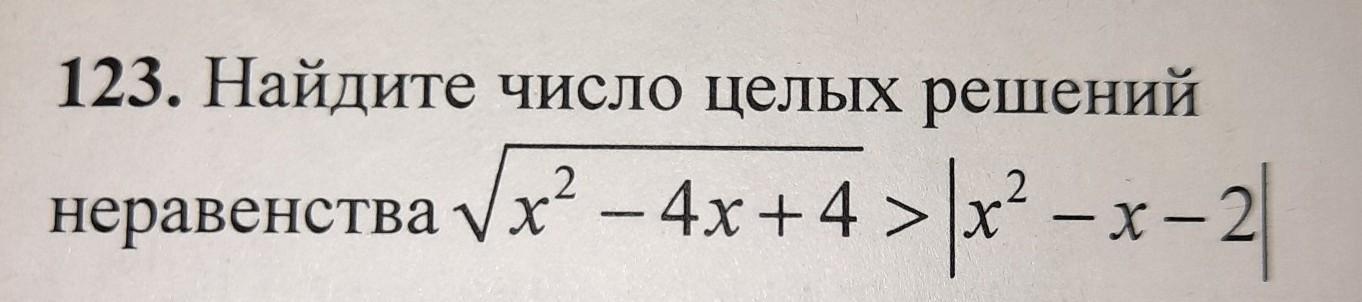Question

задание на фото. Помогите, пожалуйста.​

Answer 1

Ответ:

1

Объяснение:

√(х²-4х+4)=√(х-2)² =|x-2|;

|x-2|>|x²-x-2| используем метод рационализации для модулей. данное неравество равносильно следующему.

(x-2)²-(x²-x-2)²>0⇒(x-2-(x²-x-2))(x-2+(x²-x-2))>0, после упрощения

(x-2-x²+x+2))(x-2+x²-x-2)>0, (2х-х²)*(х²-4)>0; х*(2-х)*(х-2)*(х+2)>0;

х*(х-2)*(х-2)*(х+2)<0;   х*(х-2)²*(х+2)<0; решаем методом интервалов.

х=0; х-2=0⇒х=2; х+2=0⇒х=-2;

______-2______0_______2______

 +                 -               +                +

везде выколотые точки, т.к. неравенство строгое.

х∈(-2;0) на этом интервале одно целое решение. х=-1