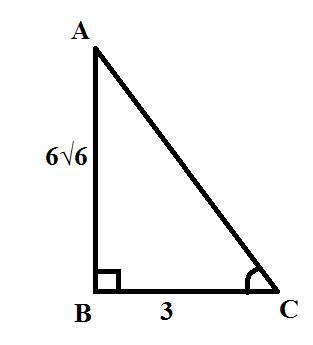
Катеты прямоугольного треугольника равны 6 и 3. Найдите косинус наибольшего острого угла этого треугольника.
и 3. Найдите косинус наибольшего острого угла этого треугольника.
Ответы
Ответ дал:
0
Напротив большей стороны лежит больший угол, следовательно нам надо найти косинус ∠С. Для этого найдём гипотенузу:
AC² = AB² + BC² = (6√6)² + 3² = 36 * 6 + 9 = 9 * (4 * 6 + 1) = 9 * 25
AC = = 3 * 5 = 15
Теперь находим косинус:
cos∠C = =
=
= 0,2
Ответ: cos∠C = или cos∠C = 0,2
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад