Question

Помогите 100 баллов Геометрия

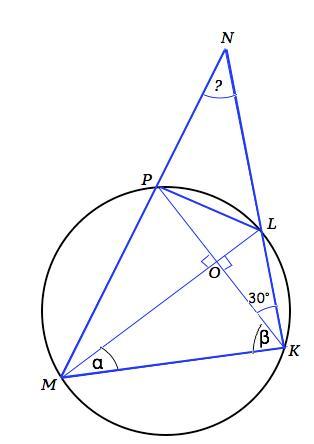
Дана окружность, пересекающая стороны MN и NK треугольника MNK в точках P и L. Вершины M и K этого треугольника лежат на данной окружности. Угол между отрезками ML и PK равен 90°, а угол PKN равен 30°. Найдите угол MNK.

Answer 1

Ответ: 30°

Объяснение:

  Вписанные ∠РМL и ∠РКL  опираются на одну хорду РL и стягивают одну дугу ⇒  они равны по свойству вписанных углов. ⇒ ∠РМL=∠PKL=30°.

  По условию ML⊥PK, поэтому   ∆ МОК  - прямоугольный. Примем острые углы этого треугольника равными  α и β , тогда  α+β=180°-90°=90°. Соседние им углы равны по 30°( доказано выше).  Поэтому в ∆ МNК ∠NМК+∠NKM= α+β+2•30°=90°+60°=150°.

  Из суммы углов треугольника искомый ∠MNK=180°-150°=30°