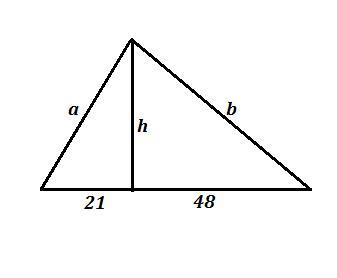
высота треугольника делит его основание на 21 и 48 см, а разница боковых сторон равна 23 см. Найдите площадь треугольника
Ответы
Ответ дал:
0
Решение.
Обозначим боковые стороны через a и b , b-a=23 .
Пусть отрезок основания в 21 см прилегает к стороне а , а отрезок в 48 см прилегает к стороне b .
Выразим высоту h треугольника, опущенную на основание с . Используем теорему Пифагора для двух прямоугольных треугольников , у которых есть общий катет h
Нашли стороны, теперь найдём высоту h , опущенную на основание с=21+48=69 и площадь треугольника .
Отdет: S=690 см² .
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад