Question

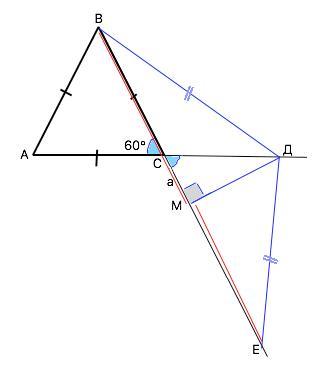
Дан правильный треугольник АВС. На продолжении стороны АС за точку С взята точка Д, а на продолжении стороны ВС за точку С - точка Е так, что ВД=ДЕ. Известно, что АД=5. Найдите СЕ.

Answer 1

Ответ: 5 ( ед. длины)

Объяснение:

По условию ВД=ДЕ. => ∆ ВДЕ - р/б.

   Пусть т. М - середина ВЕ.  Тогда ДМ - высота  и медиана ∆ ВДЕ.  В  ∆ АВС все углы=60°.

∆ СМД - прямоугольный, ∠ДСМ=∠ВСА=60° ( вертикальные), поэтому из суммы острых углов прямоугольного треугольника ∠СДМ=30°

Примем СМ=а. Тогда СД=2СМ=2а, по свойству гипотенузы в треугольнике с углом 30°

      ВМ=ЕМ=ВС+а. ⇒ ЕС=(ВС+а)+а=ВС+2а.

Но ВС+2а=АС+2а.

АД=АС+2а=5 ⇒ СЕ=АВ=5