Найдите объём тела, полученного при вращении вокруг оси
абсцисс криволинейной трапеции, ограниченной линиями
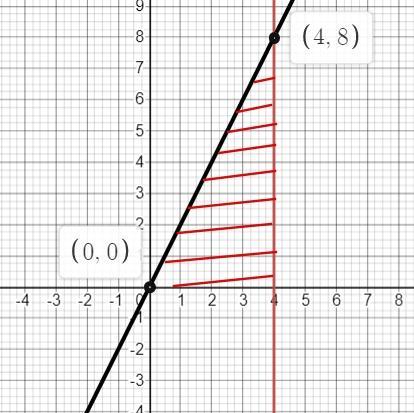
у = 2.x, x = 4, y = 0. Сделайте рисунок к задаче.
Ответы
Ответ дал:
2
Ответ:
Объяснение:
Формула для расчета
Наши пределы а = 4, b = 0
Считаем
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
9 лет назад