Ответы
Ответ дал:
0
Ответ:
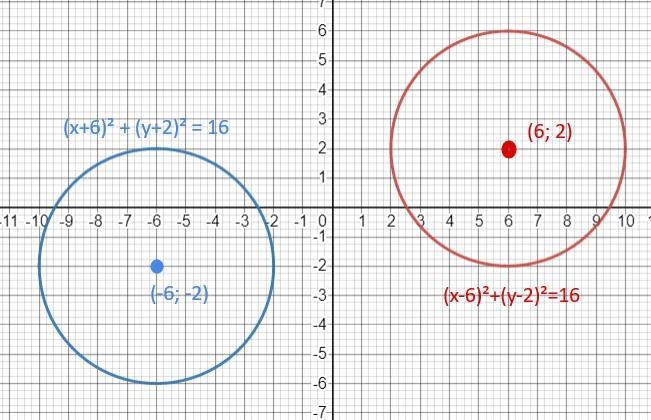
уравнение симметричной окружности (x+6)² + (y+2)² = 16
Пошаговое объяснение:
Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности.
Центр окружности (x-6)²+(y-2)²=16 - это точка с координатами (6;2). Найдём точку, симметричную ей относительно точки (0; 0).
- Две точки
и
симметричны относительно точки O(x₀;y₀), если точка O является серединой отрезка AB.
Формулы координат середины отрезка
Отсюда мы можем найти координаты нового центра окружности
(x'; y').
x' = 2*0 - 6 = -6
y' = 2*0 - 2 = -2
Таким образом, уравнение окружности будет иметь вид
(x+6)² + (y+2)² = 16
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад