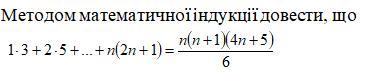Ответы
Ответ дал:
1
Объяснение:
Для n=1 утверждение , очевидно, верно 3=1*2*9/6
Обозначим сумму за S(n). Пусть утверждение верно для n
Рассмотрим выражение:
S(n+1)-S(n)=(n+1)((n+2)(4n+9)-(4n+5)*n)/6
Заметим :(4n+9)-(4n+5)=8n+18+9n-5n=12n+18
Тогда:
S(n+1)-S(n)=(n+1)*(2n+3)=(n+1)*(2*(n+1)+1)
S(n+1)=S(n)+(n+1)*(2*(n+1)+1).
Так как по предположению индукции утверждение верно для S(n), то последняя формула доказывает, что оно верно для любого n.
Anyuta8wef:
помогите пожалуйста - https://znanija.com/task/49102910
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад