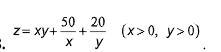Question

нужно найти найти екстремум. даю 25. желательно сдать бистро

Answer 1

Ответ: функция имеет минимум zmin=30 в точке M(5;2).

Пошаговое объяснение:

1) Находим первые производные: z'x=y-50/x²; z'y=x-20/y² и приравниваем их к нулю. Получаем систему уравнений:

y-50/x²=0

x-20/y²=0

Решая её, находим x=5 и y=2. Таким образом, найдена единственная критическая точка M(5;2).

2) Находим вторые производные: z"xx=100/x³, z"yy=40/y³, z"xy=z"yx=1 и вычисляем их значения в критической точке: A=z"xx(M)=100/125=0,8; B=z"xy(M)=z"yx(M)=1; C=z"yy(M)=5.

3) Находим значение выражения A*C-B²=3>0, поэтому функция в точке M действительно имеет экстремум, и так как при этом A>0, то это - минимум. Сам же этот минимум zmin=5*2+50/5+20/2=30.