Question

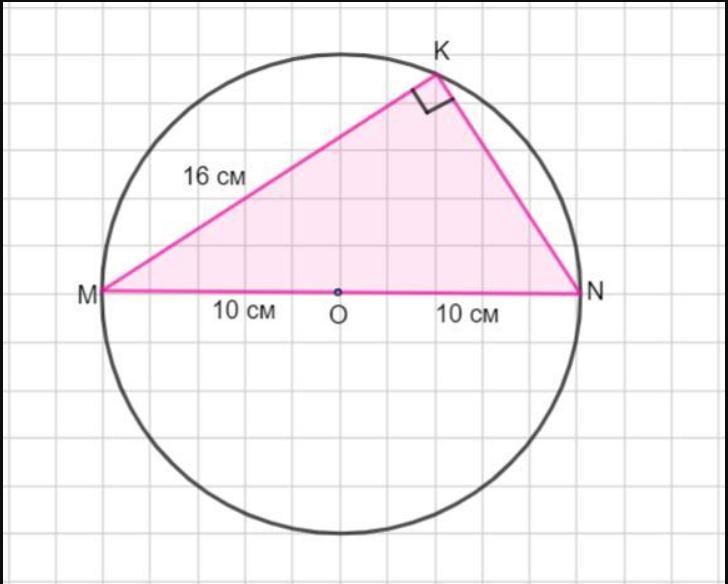
Центр окружности, описанный около треугольника MNK, лежит на стороне MN. Радиус окружности равен 10 см. Найдите NK, если MK = 16см.

Answer 1

Ответ:

NK=12 cм.

Объяснение:

Рассмотрим ΔMNK .

Данный треугольник вписан в окружность радиуса 10 см, так что центр лежит на стороне MN.

Значит, эта сторона является диаметром окружности.

MN=2R,        $MN =2\cdot10 =20$cм.

Если MN - диаметр, то вписанный угол, опирающийся на диаметр, прямой, то есть ∠MKN =90°     и ΔMNK - прямоугольный, в котором известна гипотенуза MN=20 см, а катет MK=16 см.

Найдем катет NK по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.$MN^{2} =MK^{2} +NK^{2} ;\\NK^{2} =MN^{2} -MK^{2};\\NK = \sqrt{MN^{2} -MK^{2}} ;\\NK= \sqrt{20^{2} -16^{2} } =\sqrt{(20-16)(20+16)} =\sqrt{4\cdot36} =2\cdot6=12$

Тогда NK=12 cм.

#SPJ1