100 баллов
Задана квадратичная функция y = x2 − 4x + 5.
а) Найдите координаты вершины параболы
б) Постройте график данной функции
в) Укажите промежутки возрастания и убывания данной функции
Ответы
Ответ дал:
4
Ответ:
Квадратичная ф-ция .
а) Абсцисса вершины:
Ордината вершины
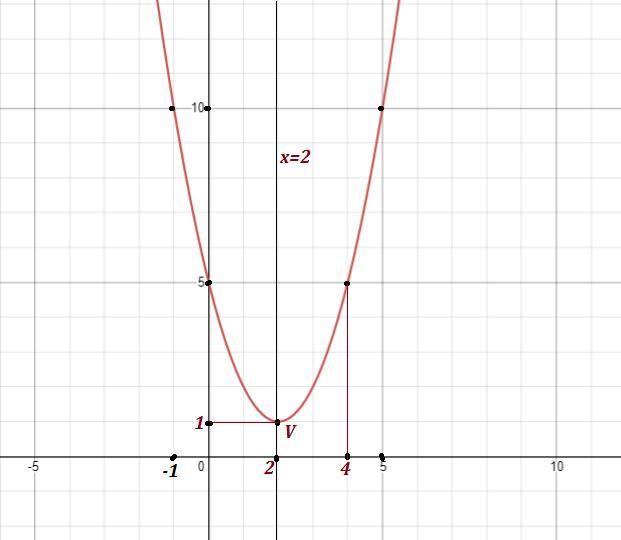
Координаты вершины V( 2 ; 1 )
Ось симметрии параболы: х=2 .
б) Точка пересечения с ОУ : (0;5) . Симметричная ей точка относительно оси х=2 - точка (4;5) .
Точек пересечения с ОХ нет .
Ещё две точки, через которую проходит график - точки (-1;10) , (5;10)
в) Промежутoк возрастания: х ∈ [ 2 ; +∞ ) .
Промежутoк убывания: х ∈ ( -∞ ; 2 ] .
Приложения:
Аноним:
здравствуйте вы не могли бы мне помочь с геометрией пожалуйста
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад