Question

Пжжж дам 100 балов
Геометрия

Answer 1

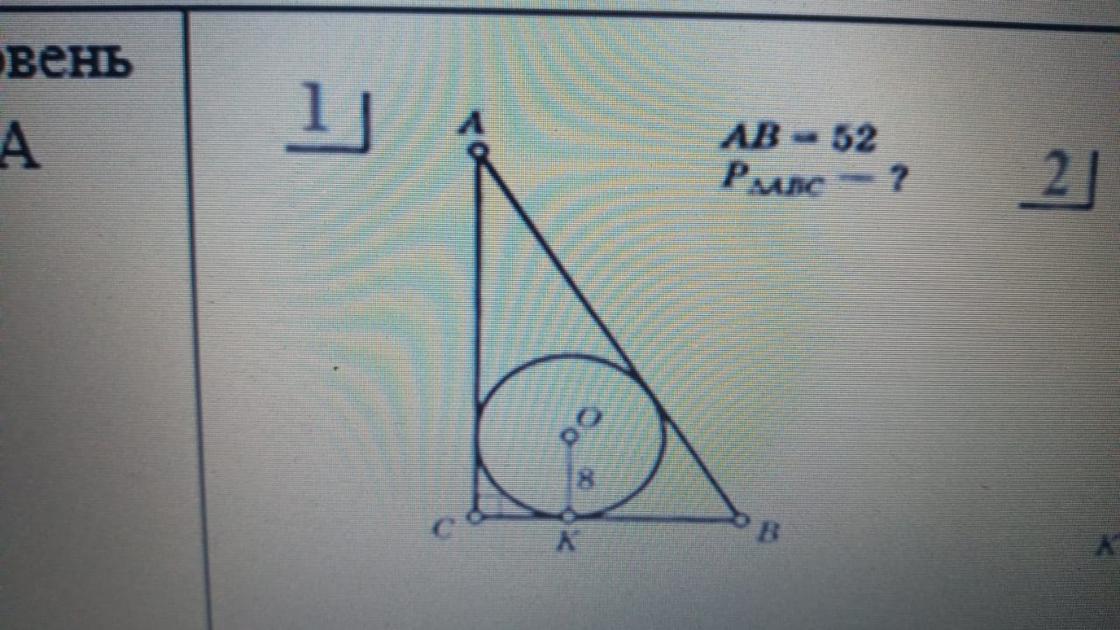
В прямоугольный треугольник , с углом ∠С=90° и гипотенузой АВ=52 см, вписана окружность радиуса 8 см. Найти периметр треугольника АВС.

Объяснение:

1) Соединим центр окружности с точками касания : А-Р-С и В-К-С. Отрезки ОР и ОК радиусы . По свойству радиуса ,проведенного в точку касания,  ОР⊥АС, ОК⊥ВС. Тогда ОРСК-прямоугольник с равными сторонами ОР и ОК ⇒ РОКС-квадрат ⇒ РС=КС=8 см.

2) По свойству отрезков касательных АР=АМ и ВК=ВМ

3) Р (АВС)=АВ+АС+ВС=52+(АР+РС)+(ВК+КС)=

=52+(АР+8)+(ВК+8)=68+(АР+ВК)=68+(АМ+ВМ)=68+52=120 (см).