Question

На координатной плоскости постройте треугольник, который задаётся неравенствами: (на фото) Найдите его площадь, если длина единичного отрезка равна 1 см. Дайте ответ в квадратных сантиметрах.​

Answer 1

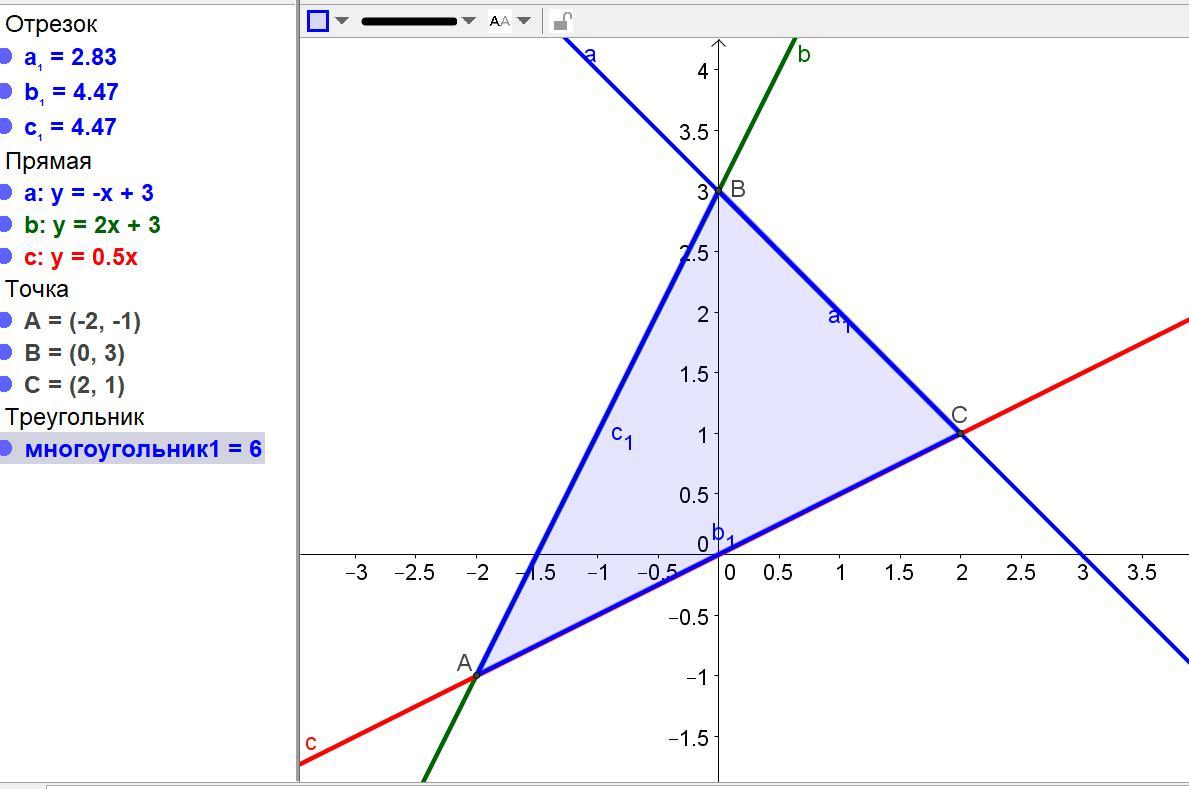
Находим координаты вершин треугольника как точки пересечения заданных прямых.

Точка А: y ≤ 2х + 3

                  y ≥ (1/2)х.

Приравняв правые стороны, получаем:

(3/2)х = -3, х = -3*2/3 = -2,

у = -2*2 + 3 = -1. А(-2; -1)

Точка В:

y ≤ -х + 3

y ≤ 2х + 3, отсюда х = 0, у = 3. В(0; 3).

Точка С: y = -х + 3

                  y = (1/2)х.  

Приравняв правые стороны, получаем:

(3/2)х = 3, х = 3*2/3 = 2,

у = -2 + 3 = 1. С(2; 1).

Формула для вычисления площади треугольника ABC по координатам его вершин имеет вид:

S = (1/2)|(x2-x1)(y3-y1) – (x3-x1)(y2-y1)|.

Подставим значения координат точек:

S = (1/2)|(0-(-2))(1-(-1)) – (2-(-2))(3-(-1))| = (1/2)|(4-16)| = 6 см².