Ответы
Ответ дал:
0
Объяснение:
а значить ділиться націло на
,
так як розклаться на множники одним з яких є
Доведно
Приложения:
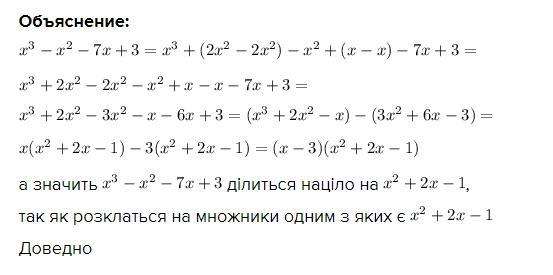
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад