Question

алгебра 9 класс, помогите, пожалуйста! ​

Answer 1

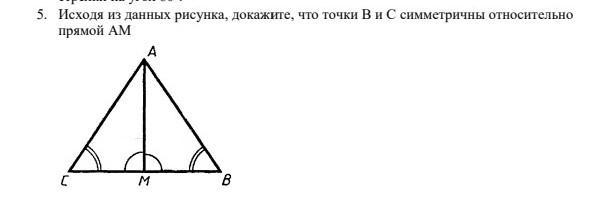
Две точки симметричны относительно прямой, называемой осью симметрии, если они лежат на прямой, перпендикулярной оси симметрии.

то есть нам надо доказать, что СВ перпендикулярна АМ.

Рассмотрим треугольник АВС.
Он равнобедренный, так как углы при основании равны.
или более точно можно доказать, что тр-к АВМ равен тр-ку АСМ (два угла равны - показаны на рисунке, значит и третий угол равен, как 180-(сумма равных углов). По 2 признаку равенства АМ общая и примыкающие углы равны. Значит АС=АВ и тр-к АВС равнобедренный.

В равнобедренном тр-ке биссектриса является медианой и восотой. АМ - биссектриса и медиана (следует из равенства тр-ков), значит и высота. И угол СМА=90. Значит АМ и ВС перпендикулярны и точки В и С симметричны.